Завдання
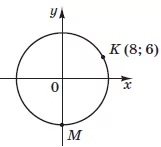
На координатній площині $$xy$$ зображено коло, центр якого збігається з початком координат (див. рисунок). Точки $$K(8;6)$$ та $$M(x;y)$$ належать цьому колу. Визначте координати точки $$M.$$
А. $$(-10;0)$$
Б. $$(10;0)$$
В. $$(0;-14)$$
Г. $$(0;-10)$$
Д. $$(0;10)$$
Рішення
Один зі способів розв’язання цього завдання – розв’язання за допомогою векторів. Заодно пропонуємо пригадати теорію з даної теми.
Знайдемо координати вектора $$\vec{OK}(8-0;6-0)=\vec{OK}(8;6)$$
Довжина вектора $$|\vec{OK}|=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$$
Значить радіус кола дорівнює 10.
Тоді стає очевидним, що координати точки $$M$$ є $$x=0$$ (точка на осі $$Oy)$$ та $$y=-10$$ (точка в нижній півплощині), тобто $$M(0;-10).$$
Аналогічного результату можна досягти під час розгляду прямокутного трикутника (необхідно опустити перпендикуляр на вісь $$Ox$$) та знаходження за теоремою Піфагора гіпотенузи, що дорівнює радіусу кола.
Відповідь: Г.