Завдання 28
Знайти найбільше значення функції $$y=\frac{(1-2\cos x)^4}{2}.$$
Рішення
Використаємо властивості косинусоїди. Областю значень косинуса є відрізок [−1; 1].
$$-1\leqslant\cos x\leqslant 1$$
Помножимо подвійну нерівність на $$-2<0,$$ змінивши при цьому знаки нерівності на протилежні. Запишемо подвійну нерівність у звичному вигляді (менше ліворуч, більше праворуч).
$$-2\leqslant -2\cos x\leqslant 2$$
Додамо 1
$$-1\leqslant 1-2\cos x\leqslant 3$$
Перед зведенням у четвертий ступінь пригадаємо такі твердження:
Перше
Нерівності $$f (x) > g (x)$$ та $$(f (x))^{2m}> (g (x))^{2m},$$ де $$m\in\mathbb{N},$$ рівносильні на тій множині $$M,$$ де $$f(x)\geqslant 0$$ й $$g(x) \geqslant 0.$$
Друге
Нерівність, обидві частини якої додатні, можна піднести до будь-якого натурального ступеня.
Зведемо в 4-й ступінь
$$0\leqslant (1-2\cos x)^4\leqslant 81$$
Розділимо на $$2>0,$$ залишивши при цьому знаки нерівності незмінними
$$0\leqslant \frac{(1-2\cos x)^4}{2}\leqslant 40.5$$
Отже, найбільше значення функції $$y$$ дорівнює $$40.5.$$
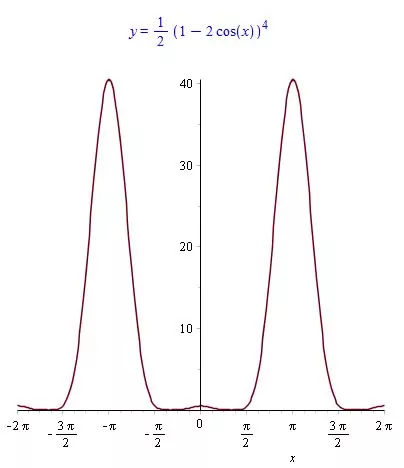
$$y=\frac{(1-2\cos x)^4}{2}.$$
Відповідь: $$40.5.$$