Завдання 17
Менша сторона прямокутника дорівнює 16 м і утворює з його діагоналлю кут $$60^{\circ}.$$ Середини всіх сторін прямокутника послідовно сполучено. Знайдіть площу утвореного чотирикутника.
А. $$256\sqrt{3}$$ м2
Б. 256 м2
В. $$64\sqrt{3}$$ м2
Г. 128 м2
Д. $$128\sqrt{3}$$ м2
Рішення
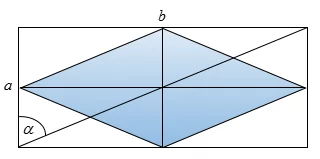
Позначимо меншу сторону прямокутника через $$a,$$ більшу через $$b,$$ а кут між діагоналлю і меншою стороною – через $$\alpha.$$
Більшу сторону прямокутника знайдемо з прямокутного трикутника, утвореного діагоналлю та двома сторонами прямокутника.
$$b=a\cdot\text{tg}\,\alpha$$ (рекомендуємо повторити визначення тригонометричних функцій)
$$b=16\cdot\text{tg}\,60^{\circ}=16\sqrt{3}$$ м
Оскільки середини сторін прямокутника з’єднані послідовно, то отриманий чотирикутник є ромбом, площу якого можна знайти через діагоналі. У нашому випадку діагоналями ромба є сторони прямокутника.
Отже, площу чотирикутника знайдемо за формулою
$$S=\frac{1}{2}ab=\frac{1}{2}\cdot16\cdot16\sqrt{3}=128\sqrt{3}$$ м2.
Відповідь: Д.