Завдання 30
У прямокутній трапеції $$ABCD\;(AD\parallel BC)$$ діагональ $$AC$$ перпендикулярна до бічної сторони $$CD.$$ Знайдіть довжину цієї діагоналі (у см), якщо $$AD=18$$ см, $$BC=8$$ см.
Рішення
З вершини $$C$$ опустимо перпендикуляр на основу $$AD$$ (див. рисунок).
Отримали $$AB=EC,$$ $$AE=BC=8$$ см, тоді $$ED=AD-AE=18-8=10$$ см.
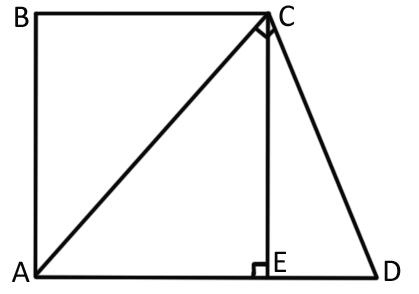
Розглянемо три прямокутні трикутники: $$\triangle ACD,$$ $$\triangle CED$$ та $$\triangle AEC.$$
За теоремою Піфагора для кожного трикутника отримаємо:
$$\left\{\begin{matrix}AC^2=AD^2-CD^2&(1)\\ CD^2=CE^2+ED^2&(2)\\ CE^2=AC^2-AE^2&(3)\end{matrix}\right.$$
Підставимо $$(3)$$ в $$(2),$$ потім отриманий результат підставимо в $$(1).$$
$$AC^2=AD^2-((AC^2-AE^2)+ED^2)$$
$$AC^2=AD^2-AC^2+AE^2-ED^2$$
$$2AC^2=AD^2+AE^2-ED^2$$
$$AC^2=\frac{1}{2}\cdot(AD^2+AE^2-ED^2)$$
$$AC=\sqrt{\frac{1}{2}\cdot(AD^2+AE^2-ED^2)}$$
Підставимо значення. Виконаємо елементарні перетворення та скористаємося властивостями коренів і степенів.
$$AC=\sqrt{\frac{1}{2}\cdot(18^2+8^2-10^2)}=\sqrt{18\cdot9+8\cdot4-10\cdot5}=\sqrt{18\cdot9+32-50}=\sqrt{18\cdot9-18}=$$
$$=\sqrt{18\cdot(9-1)}=\sqrt{18\cdot8}=\sqrt{3^2\cdot2\cdot2^3}=\sqrt{3^2\cdot4^2}=3\cdot4=12.$$
Довжина діагоналі $$AC$$ дорівнює 12 см.
Відповідь: 12.