Завдання 24
Установіть відповідність між тілом обертання, заданим умовою (1-4), і формулою (А-Д) для обчислення його об’єму $$V.$$
Умова
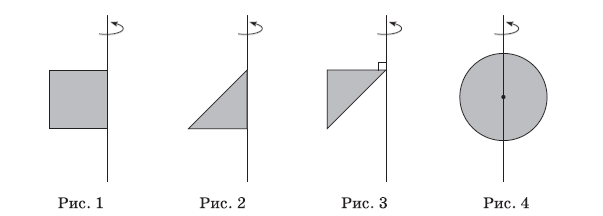
1. квадрат зі стороною $$a$$ обертається навколо прямої, що проходить через сторону цього квадрата (рис. 1)
2. прямокутний рівнобедрений трикутник із катетом $$a$$ обертається навколо прямої, що проходить через катет цього трикутника (рис. 2)
3. прямокутний рівнобедрений трикутник із катетом $$a$$ обертається навколо прямої, що проходить через вершину гострого кута цього трикутника перпендикулярно до одного з його катетів (рис. 3)
4. коло, радіус якого дорівнює $$\frac{3}{4}a,$$ обертається навколо прямої, що проходить через центр цього кола (рис. 4)
Формула
А. $$V=\frac{1}{3}\pi a^3$$
Б. $$V=\frac{9}{16}\pi a^3$$
В. $$V=\frac{2}{3}\pi a^3$$
Г. $$V=\pi a^3$$
Д. $$V=2\pi a^3$$
Рішення
1. Першій умові відповідає циліндр із висотою та радіусом, що дорівнюють $$H=R=a.$$
$$V=\pi R^2 H=\pi a^3$$
Отримали відповідність 1-Г.
2. Другій умові відповідає конус із $$H=R=a.$$
$$V=\frac{1}{3}\pi R^2 H=\frac{1}{3}\pi a^3$$
Отримали відповідність 2-А.
3. В третій з циліндра “вирізали” конус.
$$V=\pi a^3-\frac{1}{3}\pi a^3=\frac{2}{3}\pi a^3$$
Отримали відповідність 3-В.
4. В четвертій виходить сфера.
$$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi (\frac{3}{4}a)^3=\frac{9}{16}\pi a^3$$
Отримали відповідність 4-Б.