Завдання 16
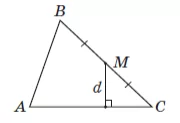
У трикутнику $$ABC$$ точка $$M$$ – середина сторони $$BC,$$ $$AC=24$$ см (див. рисунок). Знайдіть відстань $$d$$ від точки $$M$$ до сторони $$AC,$$ якщо площа трикутника $$ABC$$ дорівнює 96 см2.
А. 2 см
Б. 3 см
В. 4 см
Г. 6 см
Д. 8 см
Рішення
Площу трикутника можна обчислити за формулою $$S_{ABC}=\frac{1}{2}AC\cdot H_{AC},$$ де $$H_{AC}=H$$ – висота до сторони $$AC.$$ Знайдемо її
$$H=\frac{2\cdot S_{ABC}}{AC}=\frac{2\cdot96}{24}=8$$ см
За теоремою Фалеса $$H$$ та $$d$$ відсікають пропорційні відрізки. Отримуємо подібні трикутники (див. рисунок).
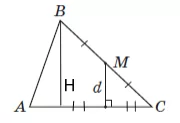
Значить $$\frac{H}{d}=\frac{BC}{MC}$$ або $$\frac{8}{d}=\frac{2MC}{MC}$$
Тоді $$d=4$$ см.
Відповідь: В.