Завдання 31
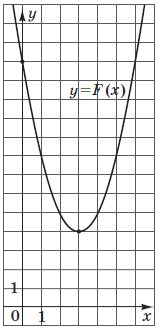
На рисунку зображено графік функції $$F(x)=x^2+bx+c,$$ яка є первісною для функції $$f(x).$$ Визначте параметри $$b$$ і $$c,$$ знайдіть функцію $$f(x).$$ У відповіді запишіть значення $$f(-5).$$
Рішення
Графік функції $$F(x)$$ перетинає вісь ординат у точці $$(0;13),$$ значить $$F(0)=c=13.$$ Вершина параболи розташована в точці $$(3;4).$$ Абсциса вершини знаходиться за формулою $$x_{B}=-\frac{b}{2a}.$$ У нашому випадку $$a=1$$ (коефіцієнт при $$x^2),$$ $$x_{B}=3.$$ Знайдемо значення $$b.$$
$$-\frac{b}{2}=3\Rightarrow b=-6$$
Тоді рівняння первісної набуває вигляду $$F(x)=x^2-6x+13.$$
Для знаходження функції $$f(x)$$ знайдемо похідну від первісної
$$f(x)=F^{\prime}(x)=2x-6$$
$$f(-5)=2\cdot(-5)-6=-16$$
Відповідь: $$-16.$$