Завдання 24
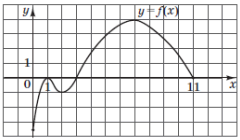
На рисунку зображено графік функції $$y=f(x),$$ визначеної на проміжку $$[0;11]$$ та диференційованої на проміжку $$(0;11).$$ Установіть відповідність між числом (1-4) та проміжком (А-Д), якому належить це число.
Число
1. найменше значення функції $$y=f(x)$$ на її області визначення
2. $$\int\limits_{1}^{3}f(x)dx$$
3. $$f(8)$$
4. $$f^{\prime}(7)$$
Проміжок
А. $$(-\infty;-2]$$
Б. $$(-2;-0.5]$$
В. $$(-0.5;2]$$
Г. $$(2;4]$$
Д. $$(4;\infty)$$
Рішення
1. Найменше значення функції на її області визначення $$[0;11]$$ дорівнює $$y=-3.5\in(-\infty; -2],$$ тобто отримали відповідність 1-А.
2. $$ -2< \int\limits_{1}^{3}f(x)dx < 0,$$ т.е. $$\int\limits_{1}^{3}f(x)dx \in(-2;-0.5]$$ і отримали відповідність 2-Б.
3. $$f(8)=3.5\in(2;4],$$ тобто отримали відповідність 3-Г.
4. Оскільки дотична до графіка функції при $$x=7$$ паралельна осі $$Ox,$$ то $$f^{\prime}(7)=k=\text{tg}\,\alpha=0\in(-0.5;2]$$ та отримали відповідність 4-В.