Завдання 31
У прямокутній системі координат зображено ескіз графіка функції $$y=\frac{x^3}{2}+x$$ і пряму, задану рівнянням $$x=a$$ (див. рисунок). При якому додатному значенні $$a$$ площа заштрихованої фігури дорівнюватиме 40 кв. од.?
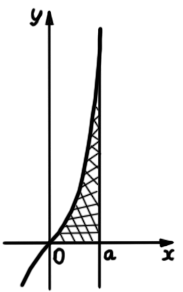
Рішення
Перша частина завдання зводиться до знаходження визначеного інтеграла $$\int\limits_{0}^{a}\left (\frac{x^3}{2}+x\right )dx$$ (пропонуємо пригадати геометричний зміст).
Під час розв’язання користуватимемося властивостями, таблицею основних невизначених інтегралів і формулою Ньютона-Лейбніца
$$S=\int\limits_{0}^{a}\left (\frac{x^3}{2}+x\right )dx=\left (\frac{x^4}{8}+\frac{x^2}{2}\right )|_{0}^{a}=\frac{a^4}{8}+\frac{a^2}{2}.$$
Перейдемо до другої частини: знайдемо значення параметра $$a >0,$$ за якого площа заштрихованої фігури дорівнює 40 кв. од.
$$\frac{a^4}{8}+\frac{a^2}{2}=40$$
$$a^4+4a^2-320=0$$
Отримали біквадратне рівняння, яке зводиться до квадратного заміною $$a^2=t >0.$$
$$t^2+4t-320=0$$
За теоремою Вієта: $$t_1=16, t_2=-20$$ (сторонній корінь)
Зворотна заміна $$a^2=16\Rightarrow a=4$$ (врахували $$a >0$$).
Відповідь: 4.