Завдання 30
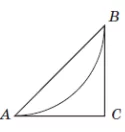
План паркової зони, обмеженої трикутником $$ABC,$$ зображено на рисунку. Дуга $$AB$$ – велосипедна доріжка. Відомо, що дуга $$AB$$ є четвертою частиною кола радіуса 1.6 км. $$CA$$ і $$CB$$ – дотичні до цього кола ($$A$$ і $$B$$ – точки дотику).
Обчисліть площу зображеної на плані паркової зони (у км2).
Рішення
Необхідно знайти площу прямокутного трикутника $$ABC.$$
$$S=\frac{1}{2}\cdot CA\cdot CB$$
Оскільки $$CA$$ та $$CB$$ – дотичні до кола відповідно в точках $$A$$ та $$B$$ і дуга $$AB$$ є четвертою частиною кола, то $$CA$$ та $$CB$$ дорівнюють між собою й дорівнюють радіусу кола, тобто $$CA=CB=1.6$$ км.
Отже, площа зображеної на плані паркової зони дорівнює
$$S=\frac{1}{2}\cdot 1.6\cdot 1.6=0.8\cdot1.6=1.28$$ км2
Відповідь: 1.28.