Завдання 22
У прямокутній системі координат на площині $$xy$$ задано точки $$O(0;0)$$ і $$A(6;8).$$ З точки $$A$$ на вісь $$x$$ опущено перпендикуляр. Точка $$B$$ – основа цього перпендикуляра. Установіть відповідність між величиною (1-4) та її числовим значенням (А-Д).
Величина
1. ордината точки $$B$$
2. довжина вектора $$\vec{OA}$$
3. довжина радіуса кола, описаного навколо трикутника $$OAB$$
4. відстань від точки $$A$$ до осі $$x$$
Числове значення
А. 0
Б. 5
В. 6
Г. 8
Д. 10
Рішення
Накреслимо рисунок
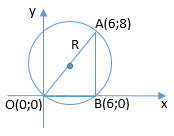
Ордината точки $$B$$ дорівнює 0. Тобто отримали відповідність 1-А.
Для знаходження довжини вектора спочатку знайдемо його координати $$\vec{OA}(6;8)$$. Довжину вектора знайдемо за формулою $$|\vec{OA}|=\sqrt{6^2+8^2}=\sqrt{100}=10.$$ Тобто отримали відповідність 2-Д.
Довжина радіуса кола, описаного біля прямокутного трикутника $$OAB,$$ дорівнює 5 ($$OA$$ – діаметр). Тобто отримали відповідність 3-Б.
Відстань від точки $$A$$ до осі $$x$$ дорівнює 8. Тобто отримали відповідність 4-Г.