Завдання 1
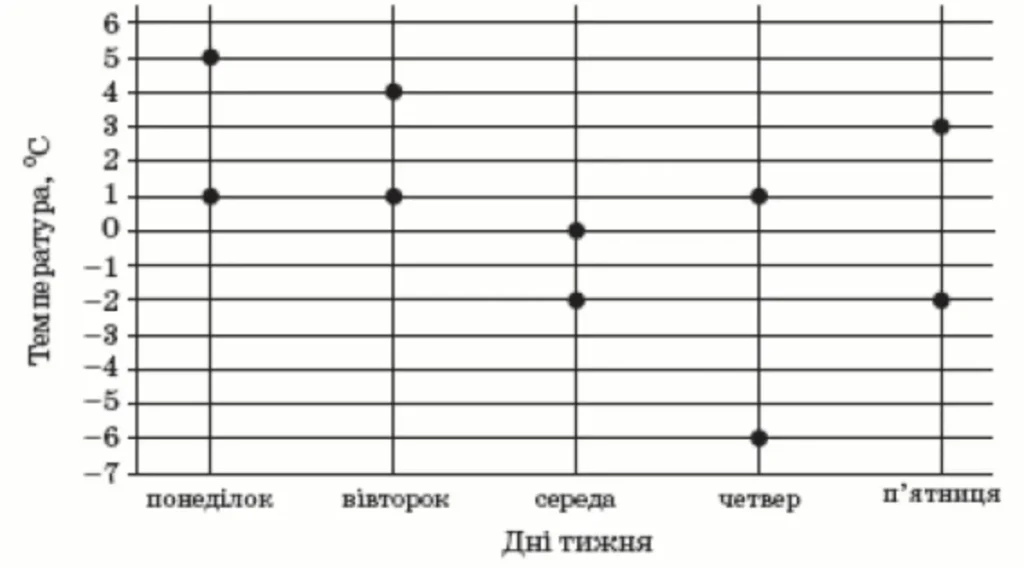
На рисунку показано жирними точками найвищу і найнижчу температури повітря кожного дня тижня з понеділка до п’ятниці в деякому місті України. По горизонталі відмічено дні тижня, а по вертикалі – температуру повітря в градусах Цельсія.
У який день різниця між найвищою та найнижчою температурами повітря була найбільшою?
| А | Б | В | Г | Д |
| Понеділок | Вівторок | Середа | Четвер | П’ятниця |
Рішення
Знайдемо різниці температур для кожного дня. Для понеділка ця різниця дорівнює: $$5-1=4;$$ для вівторка: $$4-1=3;$$ для середи: $$0-(-2)=2;$$ для четверга: $$1-(-6)=7$$ і для п’ятниці: $$3-(-2)=5.$$
Очевидно, що найбільша різниця температур була в четвер.
Відповідь: Г.
Завдання 2
Протягом тижня два кур’єри разом доставили 210 пакетів. Кількості пакетів, доставлених першим і другим кур’єрами за цей період, відносяться як 3:7. Скільки пакетів доставив другий кур’єр?
| А | Б | В | Г | Д |
| 147 | 70 | 63 | 30 | 21 |
Рішення
Для знаходження кількості пакунків, які доставив другий кур’єр, нам потрібно розділити загальну кількість доставлених пакунків на їхню суму часток і помножити на частку другого кур’єра:
$$\frac{210}{3+7}\cdot7=\frac{210\cdot7}{10}=21\cdot7=147$$
Відповідь: А.
Завдання 3
Яка з наведених точок лежить у площині $$Oxz$$ прямокутної системи координат у просторі?
| А | Б | В | Г | Д |
| $$(0;-3;0)$$ | $$(0;4;-3)$$ | $$(-3;3;3)$$ | $$(-4;3;0)$$ | $$(3;0;-4)$$ |
Рішення
Точка $$(x;y;z)$$ лежить у площині $$Oxz$$ прямокутної системи координат у просторі, якщо $$x\neq0,\;y=0,\;z\neq0.$$ Цій умові задовольняє лише точка $$(3;0;-4).$$
Відповідь: Д.
Завдання 4
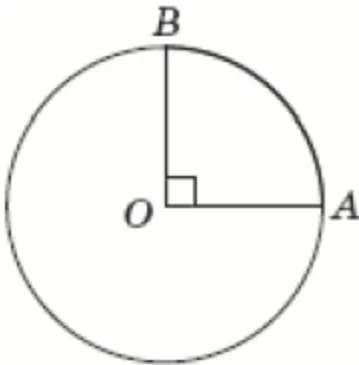
На рисунку зображено коло з центром в точці $$O$$, довжина якого дорівнює 64 см. Визначте довжину меншої дуги $$AB$$ кола, якщо $$\angle AOB=90^{\circ}.$$
| А | Б | В | Г | Д |
| 8 см | 16 см | 4 см | 32 см | 48 см |
Рішення
Згадаймо формули:
$$C=2\pi r$$ – довжина кола;
$$l=\frac{r\pi\alpha^{\circ}}{180^{\circ}}=\frac{r\pi\beta}{\pi}=r\beta$$ – довжина дуги.
$$C=64\Rightarrow 2\pi r=64\Rightarrow \pi r=32$$
$$l=\frac{r\pi90^{\circ}}{180^{\circ}}=\frac{32}{2}=16$$
Відповідь: Б.