Завдання 11
У залі кінотеатру 18 рядів. У першому ряду знаходяться 7 місць, а в кожному наступному ряду на 2 місця більше, ніж у попередньому. Скільки всього місць у залі?
| А | Б | В | Г | Д |
| 369 | 432 | 438 | 450 | 864 |
Рішення
Задача на арифметичну прогресію. Нам знадобиться наступна формула для обчислення суми 18-перших членів арифметичної прогресії:
$$S_{n}=\frac{2\cdot a_1+d\cdot (n-1)}{2}\cdot n$$
У нашому випадку $$a_1=7, d=2, n=18$$
$$s_{18}=\frac{2\cdot 7+2\cdot 17}{2}\cdot{18}=24\cdot 18=432$$
Відповідь: Б.
Завдання 12
Прямокутник зі сторонами 8 см і 10 см обертається навколо меншої сторони (див. рисунок).
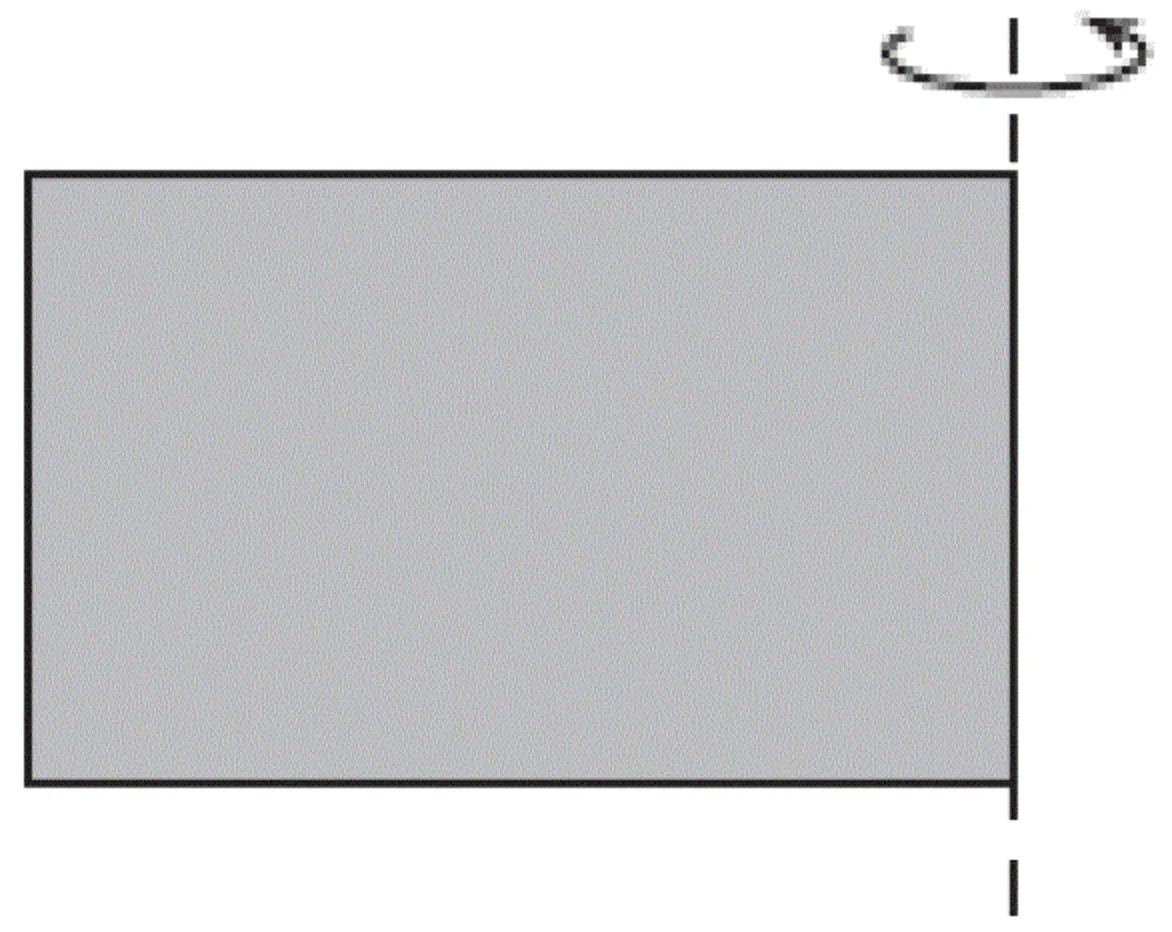
Знайдіть площу повної поверхні отриманого тіла обертання.
| А | Б | В | Г | Д |
| $$800\pi$$ см2 | $$360\pi$$ см2 | $$288\pi$$ см2 | $$260\pi$$ см2 | $$160\pi$$ см2 |
Рішення
При обертанні прямокутника навколо його сторони отримуємо циліндр. Повна площа отриманої фігури складатиметься із суми трьох площ:
$$S=S_{1}+2\cdot S_{2}$$
$$S_1$$ – площа бічної поверхні циліндра, $$S_2$$ – площа кола (основа циліндра)
$$S_{1}=2\pi RH, S_{2}=\pi R^2$$
$$S_{1}=2\pi RH, S_{2}=\pi R^2, R=10, H=8\Rightarrow$$
$$\Rightarrow S=2\pi \cdot10\cdot 8+2 \pi \cdot 10^2=360\pi$$
Відповідь: Б.
Завдання 13
Якому проміжку належить значення виразу $$\sin 410^{\circ}?$$
| А | Б | В | Г | Д |
| $$(-1;-\frac{1}{2})$$ | $$(-\frac{1}{2};\frac{1}{2})$$ | $$(\frac{1}{2};\frac{\sqrt{2}}{2})$$ | $$(\frac{\sqrt{2}}{2};\frac{\sqrt{3}}{2})$$ | $$(\frac{\sqrt{3}}{2};1)$$ |
Рішення
$$\sin 410^{\circ}=\sin(360^{\circ}+50^{\circ})=\sin 50^{\circ}$$
$$45^{\circ}<50^{\circ}<60^{\circ}, \sin 45^{\circ}= \frac{\sqrt{2}}{2},\sin 60^{\circ}= \frac{\sqrt{3}}{2} \Rightarrow \sin 45^{\circ}\in \left ( \frac{\sqrt{2}}{2};\frac{\sqrt{3}}{2} \right )$$
Оскільки на проміжку від $$0^{\circ}$$ до $$90^{\circ}$$ функція $$\sin x$$ зростає.
Відповідь: Г.
Завдання 14
З міст А і В, відстань між якими по шосе становить 340 км, одночасно назустріч один одному виїхали автобус і маршрутне таксі зі сталими швидкостями 65 км/год відповідно. Автобус і маршрутне таксі рухаються без зупинок і ще не зустрілися. За якою формулою можна обчислити відстань $$S$$ (у км) між автобусом і маршрутним таксі по шосе через $$t$$ годин після початку руху?
| А | Б | В | Г | Д |
| $$S=340-145t$$ | $$S=340-15t$$ | $$S=15t-340$$ | $$S=145t-340$$ | $$S=340+145t$$ |
Рішення
Через $$t$$ годин після початку руху автобус і маршрутне таксі проїдуть відстань, що дорівнює $$65t$$ км й $$80t$$ км відповідно, а разом $$145t$$ км. Оскільки загальна відстань $$S$$ дорівнює 340 км, то відстань між автобусом і маршрутним таксі через $$t$$ годин після початку руху можна обчислити за формулою: $$S=340-145t$$
Відповідь: А.
Завдання 15
Висота правильної чотирикутної піраміди дорівнює 4 см, а її апофема – 5 см. Визначте косинус кута між площиною бічної грані піраміди й площиною основи.
| А | Б | В | Г | Д |
| $$\frac{3}{5}$$ | $$\frac{1}{5}$$ | $$\frac{3}{4}$$ | $$\frac{4}{5}$$ | $$\frac{4}{3}$$ |
Рішення
Уведемо такі позначення: $$H$$ – висота правильної чотирикутної піраміди, $$h$$ – висота бічної грані (апофема) правильної чотирикутної піраміди, $$\alpha$$ – кут між площиною бічної поверхні піраміди та площиною основи. Розглянемо трикутник (див. рисунок)
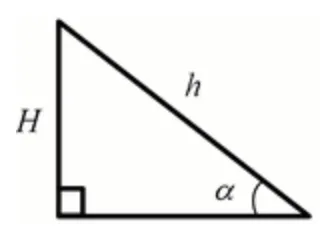
З визначення тригонометричних функцій знаходимо
$$\sin\alpha =\frac{H}{h}=\frac{4}{5},$$
тоді з основної тригонометричної тотожності знаходимо
$$\cos \alpha=\sqrt{1-\sin^2{\alpha}}= \sqrt{1-\frac{16}{25}}=\sqrt{\frac{9}{25}}=\frac{3}{5}$$
Відповідь: А.
Завдання 16
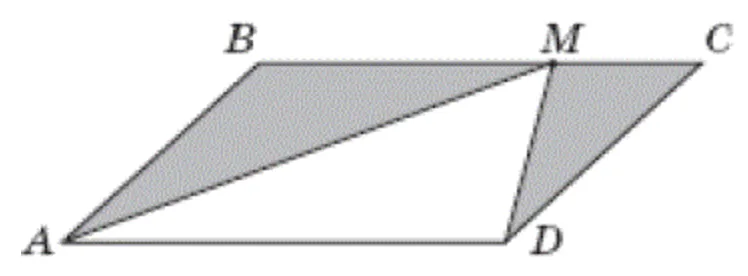
На рисунку зображено паралелограм ABCD, площа якого дорівнює 60 см2. Точка М належить стороні BC. Визначте площу фігури, що складається з двох зафарбованих трикутників.
| А | Б | В | Г | Д |
| 20 см2 | 45 см2 | 35 см2 | 40 см2 | 30 см2 |
Рішення
Від точки M до сторони AD $$(a)$$ опускаємо перпендикуляр $$h_a,$$ який є висотою трикутника AMD і паралелограма ABCD. Скористаємося формулами знаходження площ трикутника $$S_1$$ і паралелограма $$S_2$$ через висоту.
$$S_{1}=a\cdot h_{a}, S_{2}=\frac{1}{2}\cdot a\cdot h_{a}$$
$$S_{2}=60\Rightarrow S_{1}=30$$
Отже, площа фігури, що складається із зафарбованих трикутників дорівнює:
$$S_{3}=S_{2}-S_{1}=30$$
Відповідь: Д.
Завдання 17
Розв’яжіть нерівність $$(\frac{\pi}{4})^x<(\frac{4}{\pi})^3$$
| А | Б | В | Г | Д |
| $$(-3;\infty)$$ | $$(3;\infty)$$ | $$(-\infty;3)$$ | $$(-\infty;-3)$$ | $$(-\infty;\frac{1}{3})$$ |
Рішення
Перейдемо до основи $$\frac{\pi}{4}$$
$$(\frac{\pi}{4})^x<(\frac{\pi}{4})^{-3}$$
Оскільки $$\frac{\pi}{4}$$ більше нуля і менше одиниці, то знак нерівності зміниться на протилежний під час переходу до виразів, що стоять у ступенях, тобто отримаємо $$x>-3.$$
Відповідь: А.
Завдання 18
У прямокутнику ABCD: BC=80, AC=100. Через точки М і K, що належать сторонам AB і ВС відповідно, проведено пряму, паралельну АС. Знайдіть довжину більшої сторони трикутника МВК, якщо ВК=20.
| А | Б | В | Г | Д |
| 60 | 50 | 30 | 25 | 15 |
Рішення
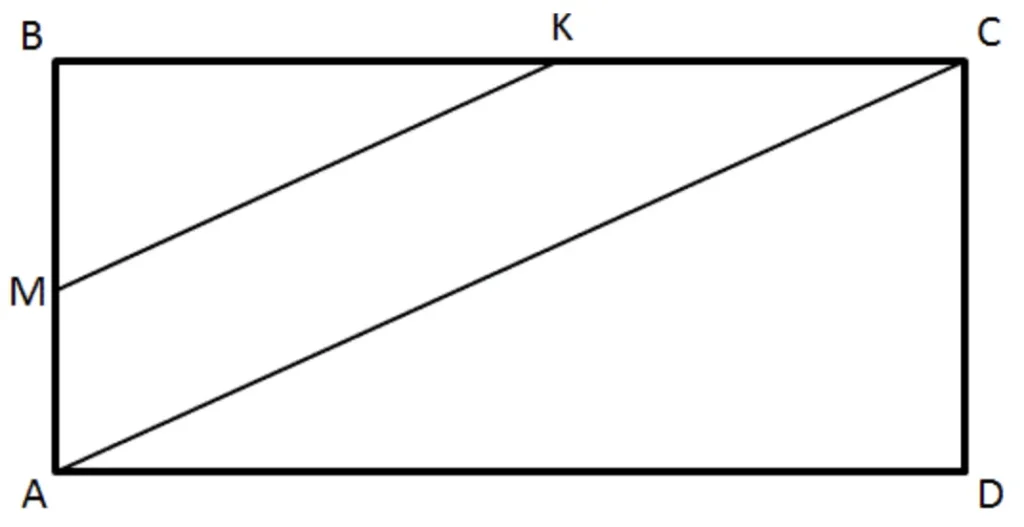
$$AC$$ – діагональ прямокутника
$$MK \parallel AC$$
$$\triangle MBK\sim \triangle ABC\Rightarrow \frac{MK}{AC}=\frac{BK}{BC}$$
$$MK=\frac{BK\cdot AC}{BC}=\frac{20\cdot 100}{80}=25$$
Відповідь: Г.
Завдання 19
Укажіть множину всіх значень $$a,$$ при яких виконується рівність $$|a^3-a^2|=a^3-a^2.$$
| А | Б | В | Г | Д |
| $$(-\infty;-1]\cup [1;\infty)$$ | $$[1;\infty)$$ | $$(-\infty;-1]\cup \left \{ 0 \right \}$$ | $$[0;1]$$ | $$\left \{ 0 \right \}\cup [1;\infty)$$ |
Рішення
$$a^3-a^2\geqslant 0\Rightarrow a^2\cdot (a-1)\geqslant 0\Rightarrow a=0, a\geqslant 1$$
Відповідь: Д.
Завдання 20
Функція $$f(x)$$ має в точці $$x_0$$ похідну $$f^{\prime}(x_{0})=-4.$$ Визначте значення похідної функції $$g(x)=2\cdot f(x)+7x-3$$ в точці $$x_0.$$
| А | Б | В | Г | Д |
| 15 | 12 | -1 | -4 | -8 |
Рішення
$$g^{\prime}(x)=2\cdot f^{\prime}(x)+7$$
$$g^{\prime}(x_{0})=2\cdot f^{\prime}(x_{0})+7=2\cdot (-4)+7=-1$$
Відповідь: В.