Завдання 1
Якщо $$m=n-1,$$ то $$7-m=$$
А. $$n-8$$
Б. $$6-n$$
В. $$8-n$$
Г. $$n-6$$
Д. $$6+n$$
Рішення
$$7-m=7-(n-1)=7-n+1=8-n$$
Відповідь: В
Завдання 2
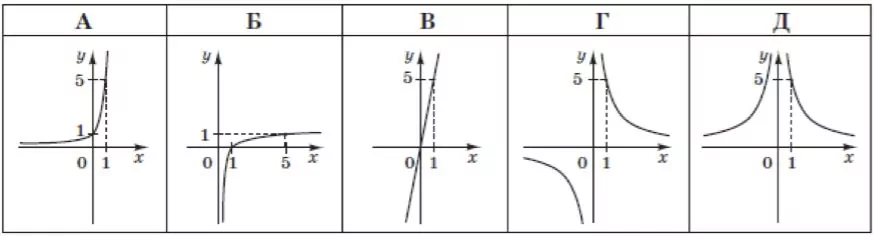
На якому рисунку зображено графік функції $$y=\frac{5}{x}?$$
Рішення
Графік функції $$y=\frac{5}{x}$$ – гіпербола з гілками, розташованими в першій і третій чвертях, що відповідає Г.
Відповідь: Г
Завдання 3
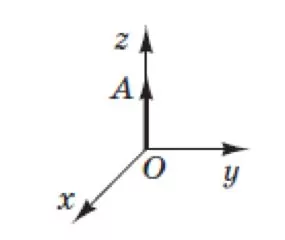
Вектор $$\vec{OA}$$ лежить на осі $$z$$ прямокутної декартової системи координат у просторі (див. рисунок), і його початок збігається з початком координат. Визначити координати вектора $$\vec{OA},$$ якщо його довжина дорівнює 3.
А. (1; 1; 1)
Б. (0; 3; 0)
В. (0; 0; 3)
Г. (3; 0; 0)
Д. (3; 3; 3)
Рішення
Оскільки вектор лежить на осі $$z,$$ то координати $$x=0$$ й $$y=0.$$ Оскільки довжина вектора дорівнює трьом і його початок співпадає з початком координат, то координата $$z=3.$$
Значить отримали $$\vec{OA}(0; 0; 3).$$
Відповідь: В
Завдання 4
Укажіть рівняння, коренем якого є число 2
А. $$\frac{1}{x-2}=0$$
Б. $$x^2+4=0$$
В. $$5x+12=2$$
Г. $$\frac{3x-6}{x}=0$$
Д. $$x+2=x$$
Рішення
Очевидно, що 2 є коренем рівняння $$\frac{3x-6}{x}=0$$
$$\frac{3\cdot2-6}{2}=\frac{0}{2}=0$$
Відповідь: Г
Завдання 5
Які з наведених тверджень є правильними?
I Сума двох будь-яких вертикальних кутів дорівнює $$180^{\circ}$$
II Сума двох будь-яких суміжних кутів дорівнює $$180^{\circ}$$
III Сума довільного гострого і довільного тупого кутів дорівнює $$180^{\circ}$$
А. Лише I
Б. Лише II
В. Лише I й III
Г. Лише II й III
Д. I, II й III
Рішення
Очевидно, що правильним є лише II твердження.
Відповідь: Б
Завдання 6
Студент на першому курсі має обрати для вивчення одну з трьох іноземних мов і для відвідування одну з п’яти спортивних секцій. Скільки всього існує варіантів вибору студентом іноземної мови та спортивної секції?
А. 5
Б. 8
В. 10
Г. 15
Д. 28
Рішення
Для знаходження всіх варіантів використовуємо правило множення
$$3\cdot5=15$$
Відповідь: Г
Завдання 7
Спростити вираз $$\frac{\sqrt[3]{64}}{64}$$
А. $$\frac{1}{16}$$
Б. $$\frac{1}{4}$$
В. $$\frac{1}{3}$$
Г. 4
Д. 16
Рішення
$$\frac{\sqrt[3]{64}}{64}=\frac{4}{64}=\frac{1}{16}$$
Відповідь: А
Завдання 8
Арифметична прогресія $$(a_n)$$ задана формулою $$n$$ члена $$a_n=4-8n.$$ Знайти різницю цієї прогресії.
А. 8
Б. 4
В. $$-2$$
Г. $$-4$$
Д. $$-8$$
Рішення
$$d=a_2-a_1$$
$$a_2=4-8\cdot2=-12$$
$$a_1=4-8\cdot1=-4$$
$$d=-12-(-4)=-8$$
Відповідь: Д
Завдання 9
Точка $$C$$ лежить на осі $$x$$ прямокутної системи координат і знаходиться на відстані 5 від точки $$A(-2;4).$$ Відрізок $$AC$$ перетинає вісь $$y.$$ Знайти координати точки $$C.$$
А. $$(1;0)$$
Б. $$(0;1)$$
В. $$(-5;0)$$
Г. $$(0;0)$$
Д. $$(3;4)$$
Рішення
Оскільки точка $$C$$ лежить на осі $$x,$$ то ордината цієї точки дорівнює нулю. $$AC$$ перетинає вісь $$y,$$ отже, абсциса додатна (відповідь А, перевіримо це). Координати вектора $$\vec{AC}(x+2;0-4).$$ Оскільки відстань (модуль вектора) дорівнює 5, то складемо і розв’яжемо рівняння:
$$(x+2)^2+16=25$$
$$(x+2)^2=9$$
$$(x+2)=3$$
$$x=1$$
Тобто координати точки $$C(1;0).$$
Відповідь: А.
Завдання 10
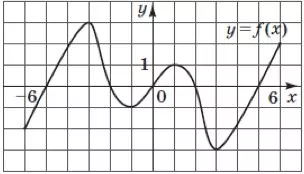
На рисунку зображено графік функції $$y=f(x),$$ визначеної на проміжку $$[-6;6].$$ Яку властивість має функція?
А. Функція є періодичною.
Б. Функція зростає на проміжку $$[-6;6].$$
В. Функція спадає на проміжку $$[-6;6].$$
Г. Функція є парною.
Д. Функція є непарною.
Рішення
На графіку присутня симетрія відносно початку координат, отже функція є непарною.
Відповідь: Д.