Завдання 9
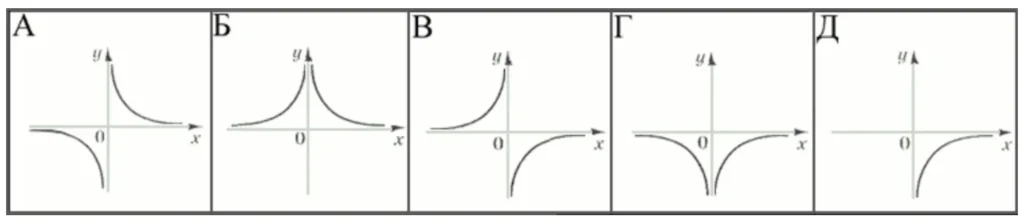
На якому з наведених рисунків зображено ескіз графіка функції $$y=-\frac{1}{x}$$?
Рішення
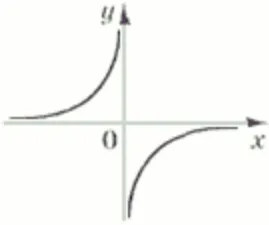
$$y=\frac{k}{x}$$ – гіпербола. При $$k>0$$ гілки розташовані в першій і третій чвертях, а при $$k<0$$ – у другій і четвертій чвертях. У нашому випадку $$k=-1$$.
Відповідь: В.
Завдання 10
Прямокутний трикутник із катетами 9 см і 12 см обертається навколо більшого катета (див. рисунок).
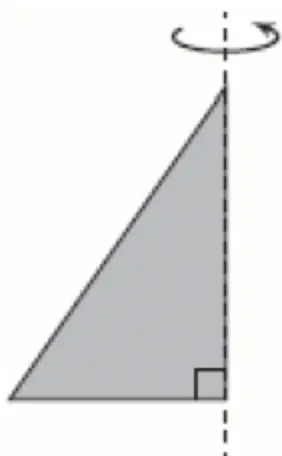
Визначте площу повної поверхні отриманого тіла обертання.
| А | Б | В | Г | Д |
| $$324\pi$$ см2 | $$216\pi$$ см2 | $$180\pi$$ см2 | $$135\pi$$ см2 | $$81\pi$$ см2 |
Рішення
У результаті обертання трикутника отримали конус. Площа повної поверхні конуса $$S$$ складається з площі бічної поверхні конуса $$S_{1}$$ та площі круга $$S_{2}$$.
$$S_{1}=\pi R l,$$ $$S_2=\pi R^2,$$ де $$R$$ – радіус основи, $$l$$ – твірна конуса.
$$R=9,\;l=\sqrt{9^2+12^2}=\sqrt{81+144}=\sqrt{225}=15$$ (за теоремою Піфагора).
$$S=\pi\cdot9\cdot15+\pi\cdot9^2=(135+81)\pi=216\pi$$.
Відповідь: Б.
Завдання 11
У магазині побутової техніки діє акція: на першу велику покупку (вартість перевищує 1000 грн) надається знижка 30 грн, на кожну наступну велику покупку попередня знижка збільшується на 25 грн. На яку за рахунком велику покупку отримає в цьому магазині покупець знижку 180 грн?
| А | Б | В | Г | Д |
| четверту | п’яту | шосту | сьому | восьму |
Рішення
Задача на арифметичну прогресію.
Перший член прогресії $$a_1=30$$, різниця прогресії $$d=25$$, $$n$$-й член $$a_n=180$$.
Знайдемо кількість $$n$$.
$$a_n=a_1+d(n-1)\Rightarrow n=\frac{a_n-a_1}{d}+1$$
$$n=\frac{180-30}{25}+1=7$$
Відповідь: Г.
Завдання 12
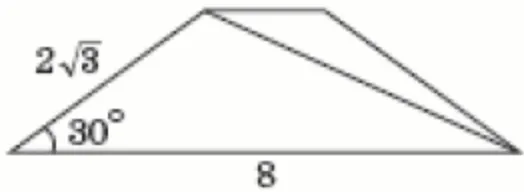
На рисунку зображено рівнобічну трапецію, бічна сторона якої дорівнює $$2\sqrt{3}$$, а більша основа – $$8$$. Визначте довжину діагоналі цієї трапеції, якщо її гострий кут дорівнює $$30^{\circ}$$.
| А | Б | В | Г | Д |
| $$\sqrt{52}$$ | $$\sqrt{76-16\sqrt{3}}$$ | $$\sqrt{76+16\sqrt{3}}$$ | $$\sqrt{28}$$ | $$\sqrt{124}$$ |
Рішення
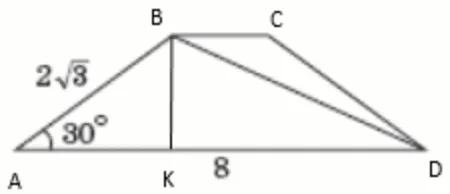
Опустимо перпендикуляр $$BK$$ на більшу основу. Отримали два прямокутні трикутники $$AKB$$ та $$DKB$$. З трикутника $$AKB$$, використовуючи визначення тригонометричних функцій і значення синуса та косинуса при $$30^{\circ}$$, знайдемо $$AK=AB\cos30^{\circ}=2\sqrt{3}\cdot\frac{\sqrt{3}}{2}=3$$ та $$BK=AB\sin30^{\circ}=2\sqrt{3}\cdot\frac{1}{2}=\sqrt{3}$$.
$$DK=AD-AK=8-3=5$$.
За теоремою Піфагора з трикутника $$DKB$$ знайдемо гіпотенузу:
$$BD=\sqrt{BK^2+DK^2}=\sqrt{3+25}=\sqrt{28}$$
Відповідь: Г.