Завдання 13
Порожній басейн, що вміщує x м3 води, повністю заповнюють водою за 5 годин (швидкість заповнення є сталою). За якою формулою можна обчислити кількість води V (у м3) у басейні через 2 години після початку його заповнення, якщо басейн був порожній і швидкість заповнення не змінювалась?
| А | Б | В | Г | Д |
| $$V=\frac{5}{2x}$$ | $$V=\frac{2}{5x}$$ | $$V=\frac{2x}{5}$$ | $$V=2\cdot5x$$ | $$V=\frac{5x}{2}$$ |
Рішення
За 1 годину можна заповнити $$V=\frac{x}{5}$$ частину басейну, а за 2 години – $$V=\frac{2x}{5}$$ частину басейну.
Відповідь: В.
Завдання 14
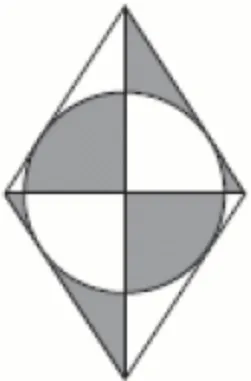
На рисунку зображено ромб, площа якого дорівнює 96 см2. У ромб вписано коло. Визначте площу зафарбованої фігури.
| А | Б | В | Г | Д |
| 32 см2 | 48 см2 | 64 см2 | 72 см2 | 24 см2 |
Рішення
Очевидно, що всі зафарбовані частини складають трикутник, площа якого дорівнює половині площі ромба. Отже, площа зафарбованої фігури дорівнює 48 см2.
Відповідь: Б.
Завдання 15
Укажіть проміжок, якому належить значення виразу $$\textup{ctg}\,25^{\circ}$$.
| А | Б | В | Г | Д |
| $$\left ( 0;\frac{1}{\sqrt{3}} \right )$$ | $$\left ( 0;\frac{\sqrt{3}}{2} \right )$$ | $$\left ( \frac{1}{\sqrt{3}};\frac{\sqrt{3}}{2} \right )$$ | $$\left ( \frac{\sqrt{3}}{2};1 \right )$$ | $$\left (\sqrt{3};\infty \right )$$ |
Рішення
Ознайомтеся з таблицею значень тригонометричних функцій.
$$\textup{ctg}\,25^{\circ}>\textup{ctg}\,30^{\circ}=\sqrt{3}$$
Відповідь: Д.
Завдання 16
Висота правильної чотирикутної піраміди дорівнює 3 см, а бічне ребро – 5 см. Визначте косинус кута між бічним ребром і площиною основи.
| А | Б | В | Г | Д |
| $$\frac{3}{4}$$ | $$\frac{1}{5}$$ | $$\frac{3}{5}$$ | $$\frac{4}{3}$$ | $$\frac{4}{5}$$ |
Рішення
Розглянемо прямокутний трикутник, у якому висота правильної чотирикутної піраміди є протилежним катетом, бічне ребро піраміди – гіпотенузою, а відрізок, який лежить в основі піраміди, – прилеглим катетом.
За теоремою Піфагора знайдемо довжину прилеглого катета: $$\sqrt{5^2-3^2}=4$$ см. З визначення тригонометричних функцій косинус кута між бічним ребром і площиною основи дорівнює: $$\cos\alpha=\frac{4}{5}$$.
Відповідь: Д.