Завдання 1
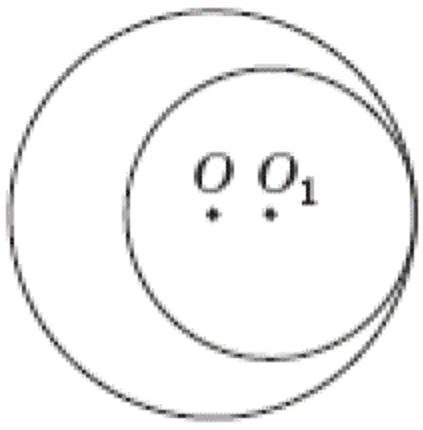
Два кола з центрами в точках $$O$$ і $$O_1$$ мають внутрішній дотик (див. рисунок).
Обчисліть відстань $$OO_1$$, якщо радіуси кіл дорівнюють 12 см і 8 см.
| А | Б | В | Г | Д |
| 4 см | 3 см | 2 см | 1.5 см | 8 см |
Рішення
$$R=12, R_{1}=8\Rightarrow OO_{1}=R-R_{1}=12-8=4$$
Відповідь: А.
Завдання 2
Знайдіть область визначення функції $$y=2-\frac{1}{x}$$.
| А | Б | В | Г | Д |
| $$(-\infty;\infty)$$ | $$(-\infty;\frac{1}{2})\cup (\frac{1}{2};\infty)$$ | $$(-\infty;0)\cup (\frac{1}{2};\infty)$$ | $$(-\infty;0)\cup (0;\infty)$$ | $$(0;\frac{1}{2})$$ |
Рішення
$$x \neq 0$$
Відповідь: Г.
Завдання 3
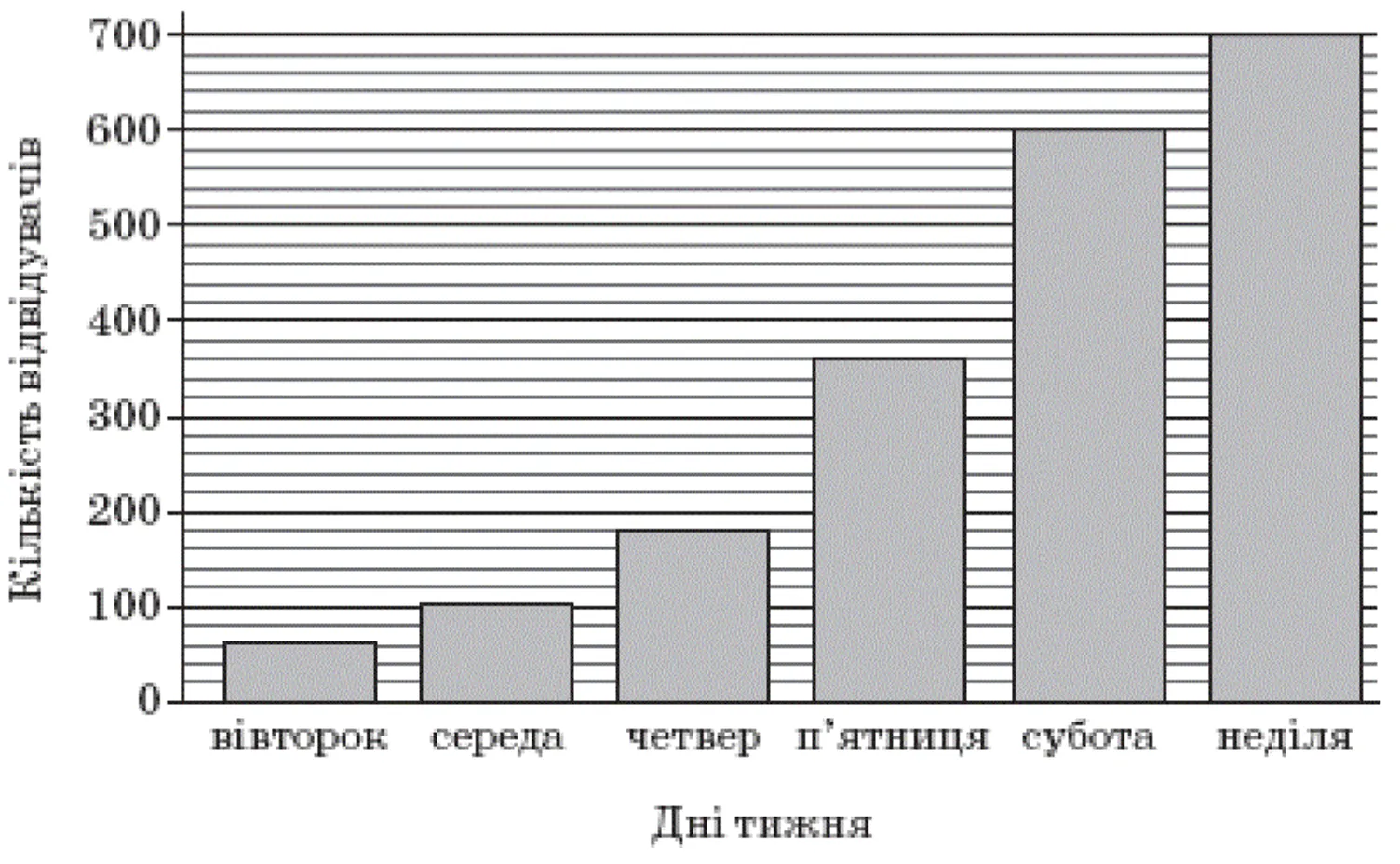
На діаграмі відображено кількість відвідувачів Музею Води протягом одного робочого тижня (з вівторка до неділі). У який день тижня кількість відвідувачів була вдвічі більшою, ніж у попередній день?
| А | Б | В | Г | Д |
| середа | четвер | п’ятниця | субота | неділя |
Рішення
1 поділці на діаграмі відповідає 20 відвідувачів. Отже, у вівторок було 60 відвідувачів, у середу – 100, у четвер – 180, у п’ятницю – 360, у суботу – 600 і в неділю – 700. Відповіддю буде п’ятниця.
Відповідь: В.
Завдання 4
Яка з наведених точок належить осі $$Oz$$ прямокутної системи координат у просторі?
| А | Б | В | Г | Д |
| $$M(0;-3;0)$$ | $$N(3;0;-3)$$ | $$K(-3;0;0)$$ | $$L(-3;3;0)$$ | $$F(0;0;-3)$$ |
Рішення
Оскільки точка повинна належати осі $$Oz$$, то $$x=0, y=0, z \neq 0$$. Цій умові задовольняє точка $$F(0;0;-3)$$.
Відповідь: Д.
Завдання 5
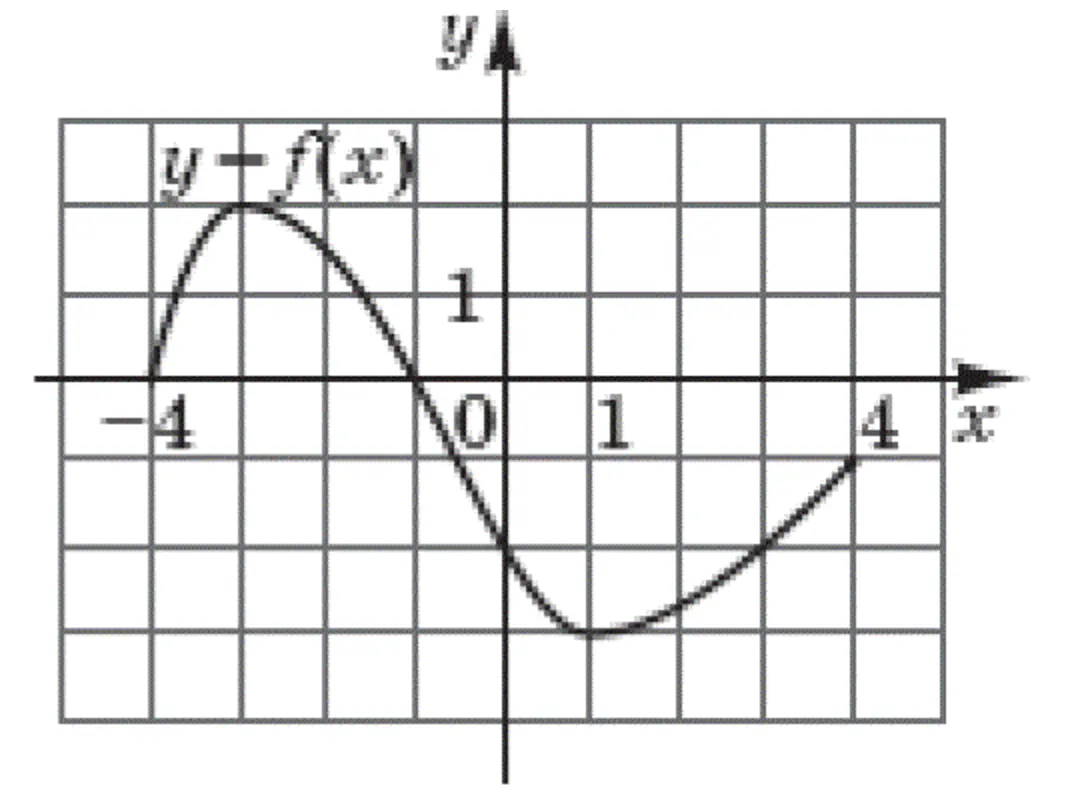
На рисунку зображено графік функції $$y=f(x)$$, визначеної на проміжку $$[-4;4]$$. Знайдіть множину всіх значень $$x$$, для яких $$f(x)\leq -2$$.
| А | Б | В | Г | Д |
| $$[-3;-2]$$ | $$[-3;2]$$ | $$[-1;4]$$ | $$[0;3]$$ | $$[-4;0]$$ |
Рішення
Якщо провести пряму $$y=-2$$, то областю розв’язків буде та частина графіка, яка нижча за цю пряму. Отримуємо $$f(x)\leq -2$$ при $$x\in [0;3]$$.
Відповідь: Г.
Завдання 6
Два фахівці розробили макет рекламного оголошення. За роботу вони отримали 5000 грн, розподіливши гроші таким чином: перший отримав четверту частину зароблених грошей, а другий – решту. Скільки гривень отримав за цю роботу другий фахівець?
| А | Б | В | Г | Д |
| 4000 грн | 3750 грн | 3000 грн | 1250 грн | 1000 грн |
Рішення
$$5000-5000\cdot \frac{1}{4}=5000\cdot(1-\frac{1}{4})=5000\cdot\frac{3}{4}=3750$$
Відповідь: Б.
Завдання 7
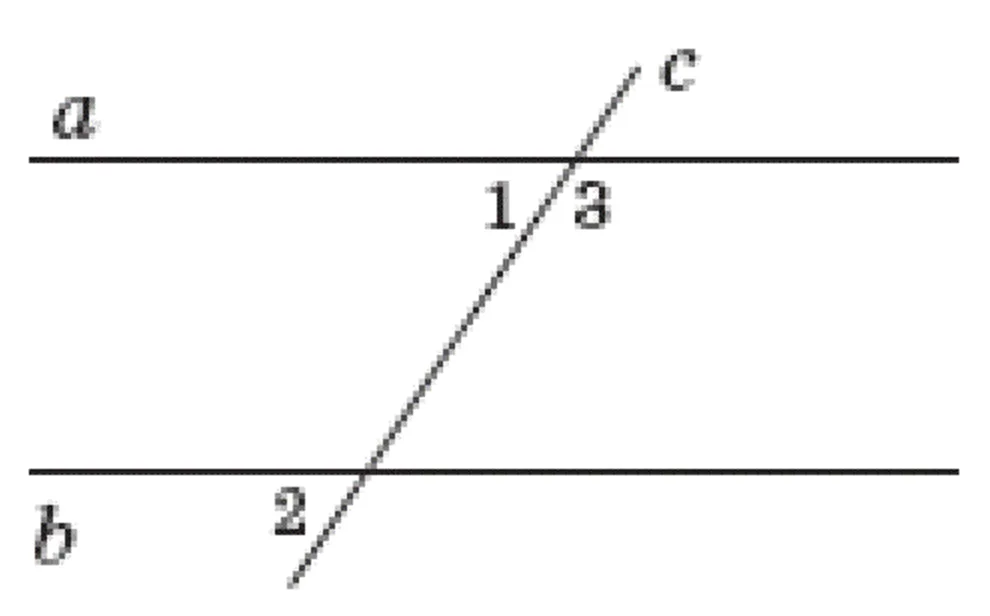
Пряма $$c$$ перетинає паралельні прямі $$a$$ і $$b$$ (див. рисунок). Які з наведених тверджень є правильними для кутів 1, 2, 3?
| А | Б | В | Г | Д |
| лише І | лише I та III | лише III | лише I та II | І, II та III |
Рішення
І. $$\angle 1$$ і $$\angle 3$$ – суміжні
II. $$\angle 1=\angle 2$$
III. $$\angle 2+\angle3=180^{\circ}$$
Відповідь: Д.
Завдання 8
Запишіть числа $$\sqrt[3]{2}, 1, \sqrt[5]{3}$$ в порядку зростання.
| А | Б | В | Г | Д |
| $$1,\sqrt[3]{2},\sqrt[5]{3}$$ | $$\sqrt[3]{2},1,\sqrt[5]{3}$$ | $$\sqrt[3]{2},\sqrt[5]{3},1$$ | $$\sqrt[5]{3},1,\sqrt[3]{2}$$ | $$1,\sqrt[5]{3},\sqrt[3]{2}$$ |
Рішення
$$\sqrt[3]{2}=\sqrt[15]{2^{5}}=\sqrt[15]{32}, 1=\sqrt[15]{1}, \sqrt[5]{3}=\sqrt[15]{3^{3}}=\sqrt[15]{27}$$
$$1<27<32\Rightarrow 1<\sqrt[5]{3}<\sqrt[3]{2}$$
Відповідь: Д
Завдання 9
При якому значенні $$x$$ вектори $$\vec{a}(2;x)$$ і $$\vec{b}(-4;10)$$ перпендикулярні?
| А | Б | В | Г | Д |
| -5 | -0.8 | 0.8 | 5 | 20 |
Рішення
Скористаємося формулами:
$$\vec{a}\perp \vec{b}\Leftrightarrow \vec{a}\cdot\vec{b}=\vec{0},(\vec{a}\neq \vec{0}, \vec{b}\neq\vec{0})$$
$$\vec{a}\cdot\vec{b}=a_{x}\cdot b_{x}+a_{y}\cdot b_{y}$$
Значить $$\vec{a}\cdot\vec{b}=2\cdot (-4)+x\cdot 10=0\Rightarrow 10x=8\Rightarrow x=0.8$$
Відповідь: В.
Завдання 10
На якому з наведених рисунків зображено ескіз графіка функції $$y=4-(x-1)^2$$ ?
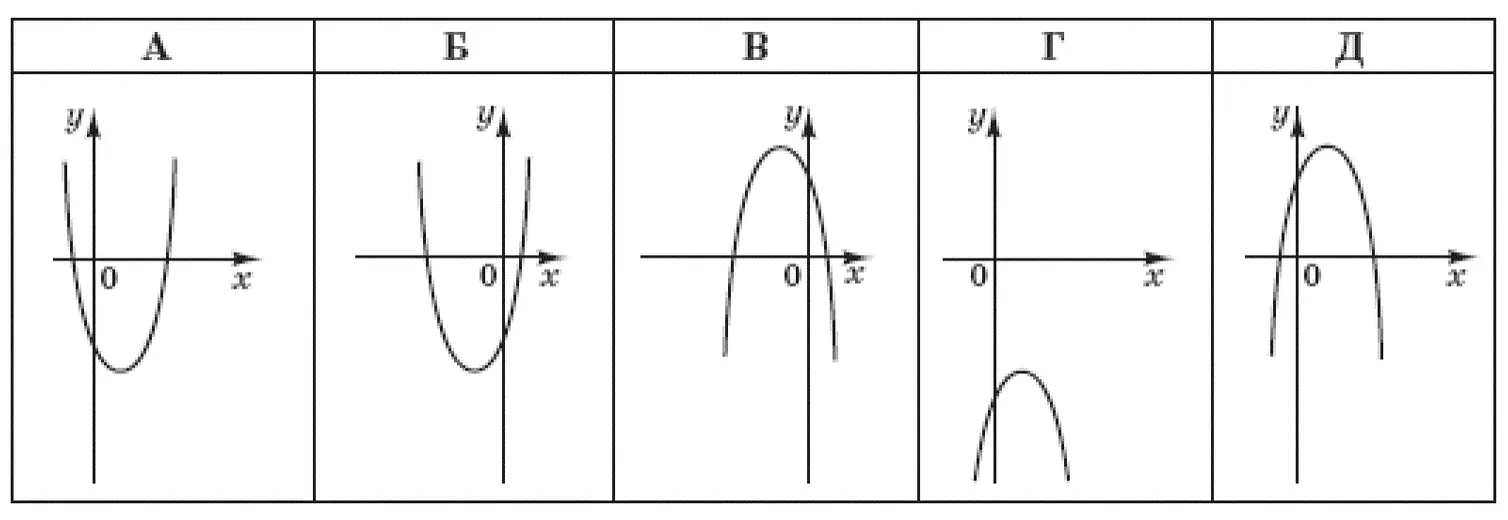
Рішення
Оскільки перед $$(x-1)^2$$ стоїть знак мінус, то гілки параболи спрямовані вниз. Вершина параболи розташована в точці $$(1;4)$$. Отже, ескіз графіка функції зображено на рисунку
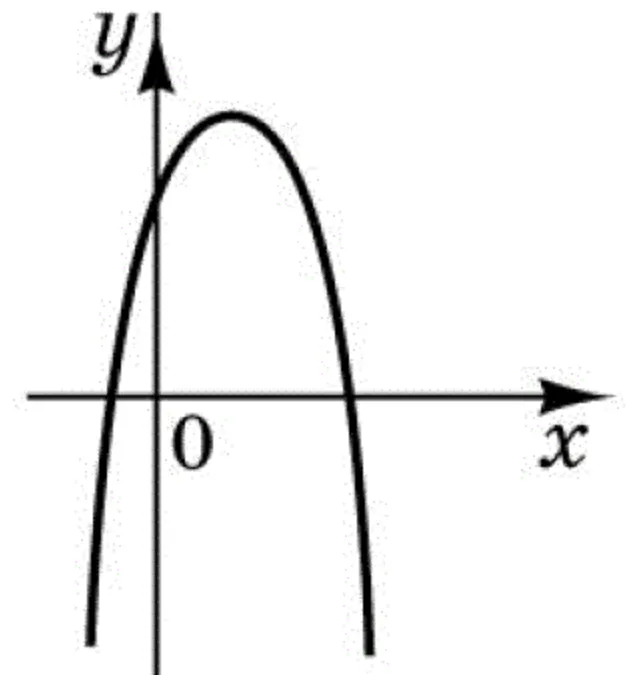
Відповідь: Д.