Завдання 11
Укажіть правильну нерівність, якщо $$a=\sin 120^{\circ}, b=\cos 120^{\circ}.$$
А. $$ 0 \lt a \lt b$$
Б. $$ a \lt 0 \lt b $$
В. $$ a \lt b \lt 0 $$
Г. $$ b \lt 0 \lt a $$
Д. $$ 0 \lt b \lt a $$
Рішення
Використовуйте формули приведення, таблицю деяких тригонометричних кутів
$$a=\sin(180^{\circ}-60^{\circ})=\sin60^{\circ}=\frac{\sqrt{3}}{2}$$
$$b=\cos(180^{\circ}-60^{\circ})=-\cos60^{\circ}=-\frac{1}{2}$$
Значить $$b \lt 0 \lt a$$
Відповідь: Г
Завдання 12
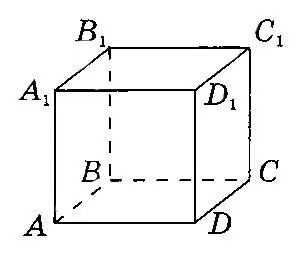
На рисунку зображено куб $$ABCDA_1B_1C_1D_1,$$ ребро якого дорівнює 1 см.
Обчислити відстань від точки $$A$$ до прямої $$B_1C_1.$$
А. 1 см
Б. 2 см
В. $$\sqrt{2}$$ см
Г. 3 см
Д. 1.5 см
Рішення
Проведемо діагональ $$AB_1\perp B_1C_1$$ – відстань від точки $$A$$ до прямої $$B_1C_1.$$
З прямокутного трикутника $$ABB_1: \angle B=90^{\circ}$$ за теоремою Піфагора
$$AB_1=\sqrt{AB^2+BB_1^2}=\sqrt{2}$$ (використали умову, що ребро куба дорівнює 1 см)
Відповідь: В
Завдання 13
Знайти всі значення $$x$$, за яких значення виразу $$2-5x$$ належить проміжку $$(-3;6).$$
А. $$ -1 < x <0.8$$
Б. $$-0.8 < x <1$$
В. $$0 < x <9$$
Г. $$-1.6 < x <0.2$$
Д. $$-0.2 < x <1.6$$
Рішення
$$-3 < 2-5x < 6$$
Віднімаємо 2
$$-5 < -5x < 4$$
Ділимо на $$-5$$, помінявши при цьому знаки нерівності на протилежні
$$-0.8 < x < 1$$
Відповідь: Б
Завдання 14
Функція $$y=f(x)$$ зростає на проміжку $$(-\infty;\infty).$$ Яке з наведених чисел може бути значенням даної функції в точці $$x=8$$, якщо $$f(1)=-2, f(9)=5?$$
А. $$-8$$
Б. $$-3$$
В. $$-2$$
Г. $$3$$
Д. $$8$$
Рішення
Оскільки функція зростає, то $$f(1) < f(8) < f(9)$$, тобто $$-2 < f(8) < 5$$
У цей інтервал із представлених потрапляє лише 3.
Відповідь: Г
Завдання 15
Довжина кола основи циліндра дорівнює $$18\pi$$ см. Визначити площу бічної поверхні цього циліндра, якщо його висота дорівнює 7 см.
А. $$126\pi$$ см2
Б. $$207\pi$$ см2
В. $$252\pi$$ см2
Г. $$288\pi$$ см2
Д. $$567\pi$$ см2
Рішення
Площу бічної поверхні циліндра можна знайти за формулою $$S=2\pi R H$$, довжину кола – за формулою $$C=2\pi R$$
Значить $$S=18\pi\cdot 7=126\pi$$
Відповідь: А
Завдання 16
$$|2-\sqrt{5}|+|2+\sqrt{5}|=$$
А. 4
Б. $$2\sqrt{5}$$
В. $$4+2\sqrt{5}$$
Г. $$4-2\sqrt{5}$$
Д. $$2\sqrt{5}-4$$
Рішення
$$2=\sqrt{4} < \sqrt{5} < \sqrt{9}=3$$
$$|2-\sqrt{5}|+|2+\sqrt{5}|=\sqrt{5} -2+2+\sqrt{5}=2\sqrt{5}$$
Відповідь: Б
Завдання 17
Крапка $$M$$ не належить площині $$\alpha.$$ Які з наведених тверджень є правильними?
I. Через точку $$M$$ можна провести лише одну площину, паралельну площині $$\alpha.$$
II. Через точку $$M$$ можна провести лише одну площину, перпендикулярну до площини $$\alpha.$$
III. Через точку $$M$$ можна провести лише одну площину, що перетинає $$\alpha$$ під кутом $$45^{\circ}.$$
А. Лише I
Б. Лише II
В. Лише I й III
Г. Лише II й III
Д. I, II й III
Рішення
Серед перерахованих правильне лише перше твердження: Через точку $$M$$, що не належить площині $$\alpha$$, можна провести лише одну площину, паралельну площині $$\alpha.$$
Відповідь: А
Завдання 18
Знайти похідну функції $$y=x^7\ln x.$$
А. $$y^{\prime}=7x^5$$
Б. $$y^{\prime}=7x^6\ln x+x^6$$
В. $$y^{\prime}=x^6\ln x+x^6$$
Г. $$y^{\prime}=7x^6\ln x$$
Д. $$y^{\prime}=7x\ln x+x^6$$
Рішення
Використовуйте правила диференціювання, таблицю похідних
$$y^{\prime}=7x^6\ln x+x^7\cdot\frac{1}{x}=7x^6\ln x+x^6$$
Відповідь: Б
Завдання 19
Об’єм конуса дорівнює 64 см3. Через середину висоти цього конуса паралельно його основі проведено площину. Одержаний переріз є основою меншого конуса, вершина якого збігається з вершиною заданого.
Знайти об’єм меншого конуса.
А. 32 см3
Б. 16 см3
В. 12 см3
Г. 8 см3
Д. 4 см3
Рішення
Об’єм конуса можна обчислити за формулою $$V=\frac{1}{3}\pi R^2 H$$
Площина, проведена через середину висоти конуса і паралельно до його основи, є у двовимірному просторі середньою лінією рівнобедреного трикутника (конус проєктується в рівнобедрений трикутник). Таким чином виходить два подібні трикутники з коефіцієнтом подібності 2.
$$V_1=64$$ – об’єм більшого конуса, $$H_1=2H_2,$$ де $$H_1$$ – висота більшого, а $$H_2$$ – меншого конуса (з умови), $$R_1=2R_2,$$ де $$R_1$$ – радіус основи більшого, а $$R_2$$ – радіус основи меншого конуса (з подібності трикутників).
Тоді $$V_2=\frac{1}{3}\pi R_2^2 H_2=\frac{1}{3}\pi (\frac{R_1}{2})^2\cdot \frac{H_1}{2}=\frac{1}{8}\cdot\frac{1}{3}\pi R_1^2 H_1=\frac{1}{8}V_1=\frac{64}{8}=8$$
Відповідь: Г
Завдання 20
Розв’язати нерівність $$3 + \log_{2}x\geqslant0.$$
А. $$[\frac{1}{8};\infty)$$
Б. $$(0;\frac{1}{8}]$$
В. $$(-\infty;\frac{1}{8}]$$
Г. $$[8;\infty)$$
Д. $$[-6;\infty)$$
Рішення
ОДЗ: $$x>0$$
$$\log_{2}x\geqslant-3$$
$$\log_{2}x\geqslant\log_{2}\frac{1}{8}$$
Основа логарифма більша за одиницю, отже, знак нерівності зберігається під час потенціювання
$$x\geqslant\frac{1}{8}$$
Відповідь: А