Завдання 5
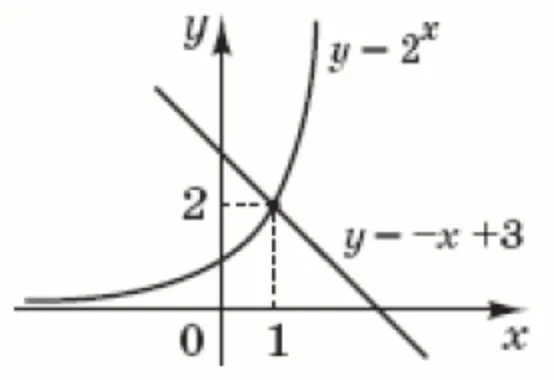
Використовуючи зображені на рисунку графіки функцій, розв’яжіть нерівність:
$$2^x>-x+3$$.
| А | Б | В | Г | Д |
| $$(1;\infty)$$ | $$(-\infty;2)$$ | $$(0;1)$$ | $$(-\infty;1)$$ | $$(2;\infty)$$ |
Рішення
Графік функції $$y=2^x$$ вище графіка функції $$y=-x+3$$ на проміжку $$(1;\infty)$$. Це і є рішення нерівності.
Відповідь: А.
Завдання 6
При якому значенні $$y$$ вектори $$\vec{a}(-3;5)$$ і $$\vec{b}(6;y)$$ колінеарні?
| А | Б | В | Г | Д |
| $$-10$$ | $$-2.5$$ | $$2.5$$ | $$3.6$$ | $$10$$ |
Рішення
У колінеарних векторів пропорційні координати.
$$\frac{-3}{6}=\frac{5}{y}\Rightarrow y=-10$$
Відповідь: А.
Завдання 7
Укажіть область визначення функції $$y=\log_{3}(x+9)$$.
| А | Б | В | Г | Д |
| $$(9;\infty)$$ | $$(-9;\infty)$$ | $$(-9;0)$$ | $$(0;\infty)$$ | $$(-\infty;\infty)$$ |
Рішення
Пропонуємо ознайомитися з логарифмами та їхніми властивостями.
Під логарифмом має бути додатне число, отже $$x+9>0\Rightarrow x>-9$$.
Відповідь: Б.
Завдання 8
Укажіть хибне твердження.
| А | Протилежні сторони паралелограма рівні. |
| Б | Сума двох кутів паралелограма, прилеглих до однієї сторони, дорівнює $$180^{\circ}$$. |
| В | Діагоналі паралелограма точкою перетину діляться навпіл. |
| Г | Площа паралелограма дорівнює половині добутку його сторони на висоту, проведену до цієї сторони. |
| Д | Площа паралелограма дорівнює добутку двох його сусідніх сторін на синус кута між ними. |
Рішення
Хибним буде твердження Г, оскільки площа паралелограма дорівнює добутку його сторони на висоту до цієї сторони.
Відповідь: Г.