Завдання 25
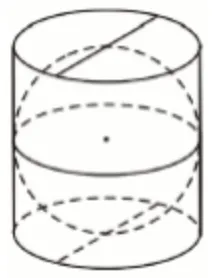
У склянку циліндричної форми, наповнену водою по самі вінця, поклали металеву кульку, що дотикається до дна склянки та стінок (див. рисунок). Визначте відношення об’єму води, яка залишилась у склянці, до об’єму води, яка вилилася зі склянки.
| А | Б | В | Г | Д |
| $$1:\pi$$ | $$2:\pi$$ | $$1:2$$ | $$2:3$$ | $$1:3$$ |
Рішення
Об’єм циліндра $$V_{1}=\pi R^2 H$$
Об’єм кулі $$V_{2}=\frac{4}{3}\pi R^3$$
У нашому випадку $$H=2R\Rightarrow V_{1}=\pi R^2\cdot2R=2\pi R^3$$
$$V_{1}-V_{2}=2\pi R^3-\frac{4}{3}\pi R^3=\frac{2}{3}\pi R^3$$
$$\frac{V_{1}-V_{2}}{V_{2}}=\frac{\frac{2}{3}\pi R^3}{\frac{4}{3}\pi R^3}=\frac{1}{2}$$
Відповідь: В.
Завдання 26
Обчисліть $$2\sqrt{13}\cos(arctg\frac{2}{3})$$
Рішення
Нехай $$arctg\frac{2}{3}=a$$, тоді $$tg a=\frac{2}{3}$$
$$\cos(arctg\frac{2}{3})=\cos a$$
Згадаймо формули: $$\cos a=\sqrt{\frac{1+\cos2a}{2}}, \cos2a=\frac{1-tg^2a}{1+tg^2a}$$
$$\cos2a=\frac{1-\left ( \frac{2}{3} \right )^2}{1+\left ( \frac{2}{3} \right )^2}=\frac{1-\frac{4}{9}}{1+\frac{4}{9}}=\frac{\frac{5}{9}}{\frac{13}{9}}=\frac{5}{13}$$
$$\cos a=\sqrt{\frac{1+\frac{5}{13}}{2}}=\sqrt{\frac{\frac{18}{13}}{2}}=\sqrt{\frac{9}{13}}=\frac{3}{\sqrt{13}}$$
$$2\sqrt{13}\cos(arctg\frac{2}{3})=2\sqrt{13}\frac{3}{\sqrt{13}}=6$$
Відповідь: 6.
Завдання 27
Обчисліть суму членів нескінченно спадної геометричної прогресії, у якої $$b_{n}=5\cdot 3^{-n}$$
Рішення:
$$b_{1}=5\cdot 3^{-1}=\frac{5}{3}, b_{2}=5\cdot 3^{-2}=\frac{5}{9}, q=\frac{b_{2}}{b_{1}}=\frac{\frac{5}{9}}{\frac{5}{3}}=\frac{1}{3}$$
$$S=\frac{b_{1}}{1-q}=\frac{\frac{5}{3}}{1-\frac{1}{3}}=\frac{\frac{5}{3}}{\frac{2}{3}}=\frac{5}{2}=2.5$$
Відповідь: 2.5
Завдання 28
Розв’яжіть рівняння $$x-5+\sqrt{2x^2-14x+13}=0$$. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток.
Рішення
$$\sqrt{2x^2-14x+13}=5-x$$
ОДЗ: $$2x^2-14x+13\geqslant 0$$
Оскільки $$\sqrt{2x^2-14x+13}\geqslant 0$$, то $$5-x\geqslant 0\Rightarrow x\leqslant 5$$
Зведемо у квадрат обидві частини рівняння:
$$2x^2-14x+13=\left (5-x \right )^2$$
$$2x^2-14x+13=25+x^2-10x$$
$$x^2-4x-12=0$$
За теоремою Вієта: $$x_{1}+x_{2}=4, x_{1}\cdot x_{2}=-12\Rightarrow x_{1}=-2, x_{2}=6$$
$$x_{2}=6>5$$ – сторонній корінь.
Виконаємо перевірку для $$x=-2$$
$$-2-5+\sqrt{2\cdot(-2)^2-14\cdot(-2)+13}=0$$
$$-7+\sqrt{8+28+13}=0$$
$$-7+\sqrt{49}=0$$
$$-7+7=0$$
$$0=0$$ – вірно
Відповідь: -2
Завдання 29
Маємо два водно-сольових розчини. Концентрація солі в першому розчині становить 0,25, а в другому − 0,4. На скільки більше треба взяти кілограмів одного розчину, ніж другого, щоб отримати розчин масою 50 кілограмів, концентрація солі в якому − 0,34.
Рішення
1 розчин: $$x$$ кг – $$0.25x$$ кг солі
2 розчин: $$y$$ кг – $$0.4y$$ кг солі
суміш: 50 кг – $$0.34\cdot50=17$$ кг солі
Складемо систему рівнянь:
$$\left\{\begin{matrix} x + y = 50\\ 0.25x + 0.4y = 17 \end{matrix}\right.$$
Виразимо $$x$$ з першого рівняння і підставимо його в друге рівняння:
$$\left\{\begin{matrix} x = 50-y\\ 0.25\cdot(50-y) + 0.4y = 17 \end{matrix}\right.$$
$$12.5-0.25y+0.4y=17$$
Для суміші в 50 кг із концентрацією солі 0.34 потрібно взяти 20 кг першого розчину і 30 кг другого, тобто на 10 кг більше.
Відповідь: 10.
Завдання 30
У коробці 80 цукерок, з яких 44 − з чорного шоколаду, а решта − з білого. Визначте ймовірність того, що навмання взята цукерка з коробки буде з білого шоколаду.
Рішення
$$P(A)=\frac{m}{n}$$
$$A$$ – цукерка з білого шоколаду
$$m=80-44=36$$ – число сприятливих результатів
$$n=80$$ – число всіх результатів
Тобто $$P(A)=\frac{36}{80}=0.45$$
Відповідь: 0.45