Завдання 25
На рисунку зображено ескіз графіка функції $$y=ax^2+bx+c.$$
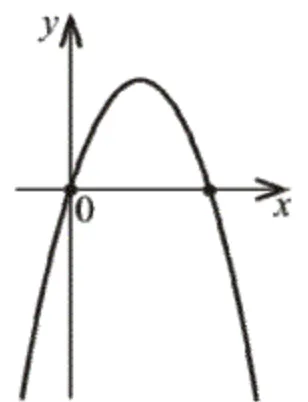
Укажіть правильне твердження щодо коефіцієнтів $$a, b, c.$$
| А | Б | В | Г | Д |
| $$\left\{\begin{matrix} a<0,\\ b<0, \\ c=0. \end{matrix}\right.$$ | $$\left\{\begin{matrix} a>0,\\ b<0, \\ c>0. \end{matrix}\right.$$ | $$\left\{\begin{matrix} a>0,\\ b>0, \\ c=0. \end{matrix}\right.$$ | $$\left\{\begin{matrix} a<0,\\ b>0, \\ c<0. \end{matrix}\right.$$ | $$\left\{\begin{matrix} a<0,\\ b>0, \\ c=0. \end{matrix}\right.$$ |
Рішення
$$y=ax^2+bx+c$$ – парабола.
При $$a>0$$ гілки параболи спрямовані вгору, при $$a<0$$ – вниз.
Оскільки гілки нашої параболи спрямовані вниз, то $$a<0$$
Якщо $$a$$ та $$b$$ з однаковими знаками, то вершина параболи розташована в лівій півплощині; якщо знаки різні, то в правій півплощині.
Оскільки вершина розташована в правій півплощині та $$a<0,$$ то отримуємо $$b>0$$
$$c=y(0)$$
Одна з точок перетину $$(0;0),$$ тобто $$y(0)=0,$$ отже, $$c=0$$
Відповідь: Д.
Завдання 26
Установіть відповідність між числом (1-4) та множиною, до якої воно належить (А-Д).
| 1 | $$-8$$ | А | множина парних натуральних чисел |
| 2 | 23 | Б | множина цілих чисел, що не є натуральними числами |
| 3 | $$\sqrt{16}$$ | В | множина раціональних чисел, що не є цілими числами |
| 4 | 1.7 | Г | множина ірраціональних чисел |
| Д | множина простих чисел |
Рішення
$$-8$$ – ціле, але не натуральне
23 – просте число
$$\sqrt{16}=4$$ – парне натуральне число
1.7 – раціональне дробове число
Відповідь: 1-Б, 2-Д, 3-А, 4-В.
Завдання 27
Установіть відповідність між функціями, заданими формулами (1-4), та їхніми властивостями (А-Д).
| 1 | $$y=x^3$$ | А | областю визначення функції є проміжок $$[0;\infty)$$ |
| 2 | $$y=\cos x$$ | Б | функція спадає на інтервалі $$(0;\infty)$$ |
| 3 | $$y=\text{tg}\, x$$ | В | функція зростає на інтервалі $$(-\infty;\infty)$$ |
| 4 | $$y=\log_{0.2} x$$ | Г | парна функція |
| Д | періодична функція з найменшим періодом $$T=\pi$$ |
Рішення
$$y=x^3$$ – зростає на інтервалі $$(-\infty;\infty)$$
$$y=\cos x$$ – періодична парна функція
$$y=\text{tg}\, x$$ – періодична з найменшим періодом $$T=\pi$$
$$y=\log_{0.2} x$$ – (основа менша за одиницю) убуває на інтервалі $$(0;\infty)$$
Відповідь: 1-В, 2-Г, 3-Д, 4-Б.
Завдання 28
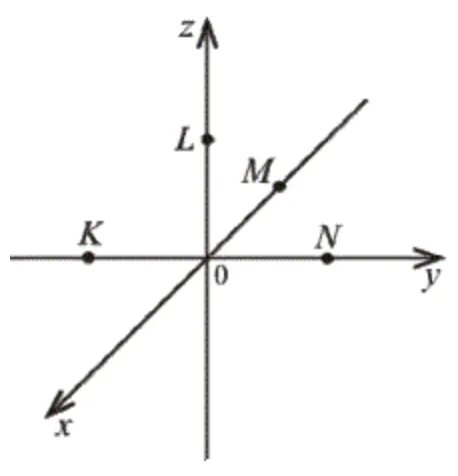
На рисунку зображено прямокутну систему координат у просторі, на осях якої позначено точки $$K,L,M,N.$$ Установіть відповідність між точками $$K,L,M,N$$ (1-4) та їхніми можливими координатами (А-Д).
| 1 | $$K$$ | А | $$(-3;0;0)$$ |
| 2 | $$L$$ | Б | $$(0;-3;0)$$ |
| 3 | $$M$$ | В | $$(0;0;-3)$$ |
| 4 | $$N$$ | Г | $$(0;0;3)$$ |
| Д | $$(0;3;0)$$ |
Рішення
Координати записуються таким чином: $$(x;y;z)$$
$$K(0;-3;0), L(0;0;3), M(-3;0;0), N(0;3;0)$$
Відповідь: 1-Б, 2-Г, 3-А, 4-Д.
Завдання 29
Знайдіть значення виразу $$\frac{m+4}{m^2-6m+9}\cdot \frac{2m-6}{m^2-16}-\frac{2}{m-4},$$ якщо $$m=4.25.$$
Рішення
$$\frac{m+4}{(m-3)^2}\cdot \frac{2m-6}{(m-4)(m+4)}-\frac{2}{m-4}=\frac{2}{(m-3)(m-4)}-\frac{2}{m-4}=$$
$$=\frac{2-2m+6}{(m-3)(m-4)}=\frac{2(4-m)}{(m-3)(m-4)}=\frac{2}{3-m}$$
підставимо $$m=4.25$$
$$\frac{2}{3-4.25}=-1.6$$
Відповідь: $$-1.6.$$
Завдання 30
Одним із мобільних операторів було запроваджено акцію “Довше розмовляєш – менше платиш” з такими умовами: плата за з’єднання відсутня; за першу хвилину розмови абонент сплачує 30 коп., а за кожну наступну хвилину розмови – на 3 коп. менше, ніж за попередню; плата за одинадцяту та всі наступні хвилини розмови не нараховується; умови дійсні для дзвінків абонентам усіх мобільних операторів країни.
Скільки за умовами акції коштуватиме абоненту цього мобільного оператора розмова тривалістю 8 хвилин (у грн)?
Рішення
Задача на арифметичну прогресію.
Скористаємося формулою суми перших $$n$$ членів арифметичної прогресії в такому вигляді:
$$S_{n}=\frac{2a_{1}+d(n-1)}{2}\cdot n$$
У нашому випадку: $$a_{1}=30, d=-3, n=8$$
$$S_{8}=\frac{2\cdot30+(-3)(8-1)}{2}\cdot 8=156$$ (коп.)$$=1.56$$ (грн)
Відповідь: 1.56 грн.