Визначення
Степеневою функцією називається функція вигляду $$y=x^{\alpha}.$$
Види графіків степеневої функції залежно від $$\alpha:$$
1. $$\alpha=n$$ ($$n\geqslant2$$ – натуральне число).
Така степенева функція визначена при будь-яких значеннях змінної $$x.$$
Графік функції $$y=x^n$$ проходить через точку $$(1;1)$$ і дотикається осі абсцис у початку координат.
Графік при парних $$n$$
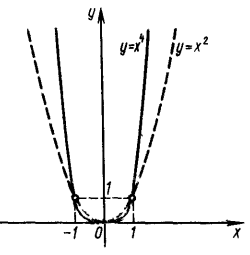
$$y=x^2, y=x^4.$$
Графік при непарних $$n$$
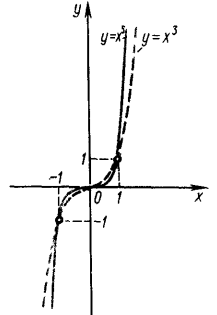
$$y=x^3, y=x^5.$$
2. $$\alpha=-n$$ $$(n\in \mathbb{N}).$$
Така степенева функція визначена при $$x\in(-\infty;0)\cup(0;\infty).$$ Графік функції $$y=\frac{1}{x^n}$$ проходить через точку $$(1;1).$$
Графіки функцій при $$n=1, n=2, n=3$$
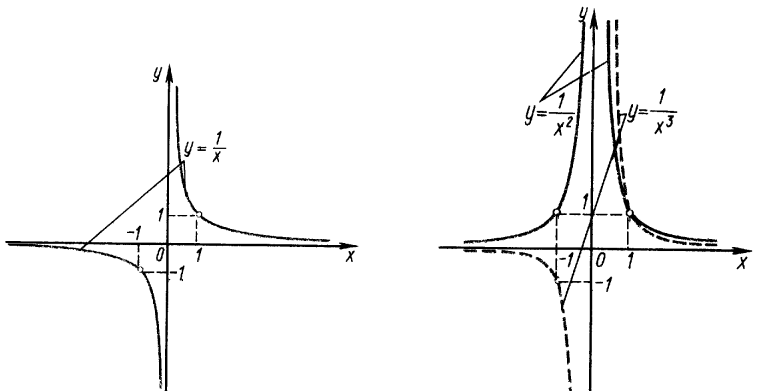
$$y=\frac{1}{x}, y=\frac{1}{x^2}, y=\frac{1}{x^3}.$$
3. $$\alpha=r$$ ($$r=\frac{m}{n},$$ $$m$$ та $$n$$ – взаємно прості натуральні числа).
Така степенева функція має нуль в початку координат, а її графік проходить через точку $$(1;1).$$ При парному $$n$$ степенева функція $$y=x^{\frac{m}{n}}$$ визначена на множині $$[0;\infty),$$ а при непарному $$n$$ – на множині $$\mathbb{R}$$ всіх дійсних чисел.
Графіки функцій при різних $$m$$ та $$n$$
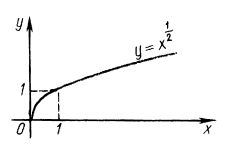
$$y=x^{\frac{1}{2}}.$$
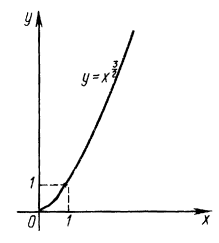
$$y=x^{\frac{3}{2}}.$$
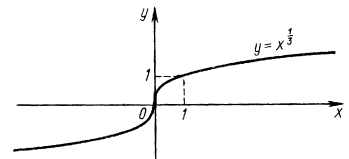
$$y=x^{\frac{1}{3}}.$$
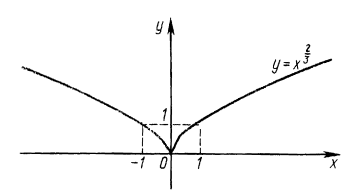
$$y=x^{\frac{2}{3}}.$$
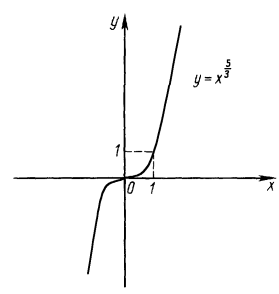
$$y=x^{\frac{5}{3}}.$$
4. $$\alpha=q$$ ($$q=\frac{m}{n} <0,$$ $$m$$ та $$n$$ – взаємно прості цілі числа, $$n\neq-1$$).
При парному $$n$$ функція, визначена на множині $$(0;\infty),$$ а при непарному $$n$$ – на множині $$(-\infty;0)\cup(0;\infty).$$ Графік функції проходить через точку $$(1;1).$$
Графіки при різних $$m$$ та $$n$$
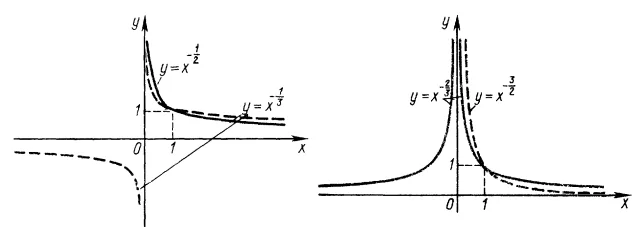
$$y=x^{-\frac{1}{2}}, y=x^{-\frac{1}{3}}, y=x^{-\frac{2}{3}}, y=x^{-\frac{3}{2}}.$$