Пропонуємо Вашій увазі розв’язання тестових завдань третьої частини першого варіанта ДПА 2012 з математики для одинадцятого класу.
Третя частина атестаційної роботи складається з трьох завдань відкритої форми з розгорнутою відповіддю. Розв’язання завдань 3.1 – 3.3 має містити пояснення. У ньому необхідно записати послідовні логічні дії та пояснення, послатися на математичні факти, з яких випливає те чи інше твердження. За необхідності розв’язки ілюструються схемами, графіками, таблицями.
Завдання 3.1
Обчислити значення виразу $$\log_2\left ( \log_3 \cos\frac{\pi}{6}-\log_3 \sin\frac{\pi}{6}\right )$$.
Рішення
Скористаємося властивостями логарифмів, визначенням і таблицею значень деяких кутів тригонометричних функцій.
$$\log_2\log_3\textup{ctg}\,\frac{\pi}{6}=\log_2\log_3\sqrt{3}=\log_2\frac{1}{2}=-1$$
Відповідь: $$-1$$.
Завдання 3.2
Знайти координати точки на прямій $$y=2-7x$$, якщо різниця квадратів абсциси та ординати цієї точки є найбільшою.
Рішення
Нехай $$A(x;y)$$ – шукана точка. Розглянемо функцію різниці квадратів абсциси та ординати цієї точки $$f(x;y)=x^2-y^2$$.
За умовою $$y=2-7x$$. Підставимо у функцію $$f(x;y)$$ і отримаємо функцію, що залежить тільки від однієї змінної $$x$$.
$$f(x)=x^2-(2-7x)^2$$
Перетворимо отриману функцію, використовуючи формулу квадрат різниці та приведення подібних доданків
$$f(x)=x^2-(4+49x^2-28x)=x^2-4-49x^2+28x=-48x^2+28x-4$$
Оскільки за умовою різниця квадратів абсциси й ординати точки $$A(x;y)$$ має бути найбільшою, то знайдемо найбільше значення функції $$f(x)$$. Для цього знайдемо похідну цієї функції.
$${f}^{\prime}(x)=-96x+28$$
Знайдемо значення змінної, в яких похідна дорівнює нулю $${f}^{\prime}(x)=0$$.
$$-96x+28=0\Rightarrow x=\frac{7}{24}$$.
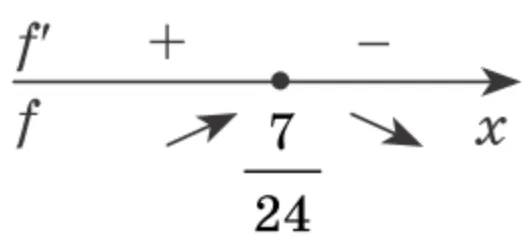
При $$x=\frac{7}{24}$$ функція $$f(x)$$ набуває найбільшого значення. Підставимо його в рівняння прямої: $$y\left (\frac{7}{24} \right )=2-\frac{49}{24}=\frac{48-49}{24}=-\frac{1}{24}$$.
$$A\left (\frac{7}{24};-\frac{1}{24} \right )$$ – шукана точка.
Відповідь: $$A\left (\frac{7}{24};-\frac{1}{24} \right )$$.
Завдання 3.3
Висота конуса дорівнює діаметру його основи. Знайти відношення площі його основи до площі бічної поверхні.
Рішення
Розглянемо осьовий переріз конуса. Отримали рівнобедрений трикутник $$ASB$$. За умовою висота конуса $$SO$$ (вона ж висота трикутника $$ASB$$) дорівнює діаметру основи конуса $$AB$$.
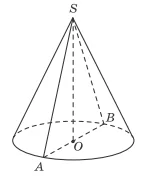
Розглянемо прямокутний трикутник із трикутника $$SOA:\;\angle SOA=90^{\circ}.$$ Нехай $$AB=SO=x$$, тоді $$AO=\frac{x}{2}$$. За теоремою Піфагора знайдемо гіпотенузу $$AS$$, яка є бічною стороною в трикутнику $$ASB$$.
$$AS=\sqrt{x^2+\frac{x^2}{4}}=\sqrt{\frac{5x^2}{4}}=\frac{x\sqrt{5}}{2}$$.
Площа основи конуса обчислюється як площа круга
$$S_1=\pi R^2=\pi AO^2=\frac{x^2\pi}{4}$$.
Площа бічної поверхні конуса обчислюється за формулою
$$S_2=\pi\cdot R\cdot l=\pi \cdot AO\cdot AS=\pi\cdot\frac{x}{2}\cdot\frac{x\sqrt{5}}{2}=\frac{\pi x^2\sqrt{5}}{4}$$.
Знайдемо відношення площі основи конуса до площі його бічної поверхні
$$\frac{S_1}{S_2}=\frac{\frac{\pi x^2}{4}}{\frac{\pi x^2\sqrt{5}}{4}}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$$.
Відповідь: $$\frac{\sqrt{5}}{5}$$.
Джерело: Збірник завдань для державної підсумкової атестації з математики: 11 кл. / О.С. Істер, О.І. Глобін, О.В. Комаренко. – К.: Центр навч.-метоод. л-ри, 2012.