Завдання 8
Журнал коштував 25 грн. Через два місяці цей самий журнал став коштувати 21 грн. На скільки відсотків знизилася ціна журналу?
| А | Б | В | Г | Д |
| $$4\%$$ | $$\frac{4}{21}\cdot 100\%$$ | $$\frac{25}{21}\cdot 100\%$$ | $$84\%$$ | $$16\%$$ |
Рішення
Складемо пропорцію
$$\begin{matrix} 25 &= &100\% \\ (25-21) &=& x\% \end{matrix}$$
$$\Rightarrow x=\frac{100\%\cdot 4}{25}=16\%$$
Відповідь: Д.
Завдання 9
На одиничному колі зображено точку $$P(-0.8;0.6)$$ і кут $$\alpha$$ (див. рисунок). Визначте $$\cos\alpha.$$
| А | Б | В | Г | Д |
| $$-0.8$$ | $$0.6$$ | $$0.8$$ | $$-0.6$$ | $$-\frac{\sqrt{3}}{2}$$ |
Рішення
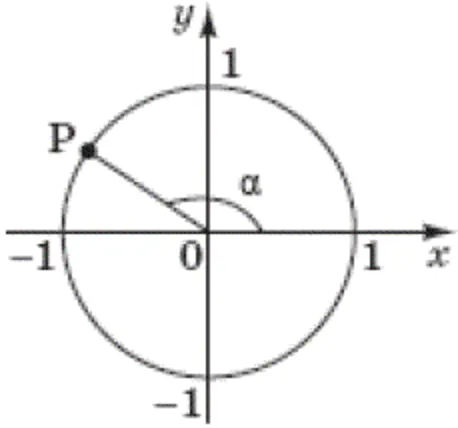
З визначення тригонометричних функцій на одиничному колі:
$$\cos\alpha=x,$$ $$\sin\alpha=y,$$ $$\text{tg}\alpha=\frac{y}{x}, (\alpha\neq\frac{\pi}{2}+k\pi),$$ $$\text{ctg}\alpha=\frac{x}{y}, (\alpha\neq\pi k), k\in \mathbb{Z}.$$
$$x=-0.8\Rightarrow \cos\alpha=-0.8$$
Відповідь: А.
Завдання 10
Знайдіть градусну міру внутрішнього кута правильного десятикутника.
| А | Б | В | Г | Д |
| $$18^{\circ}$$ | $$36^{\circ}$$ | $$72^{\circ}$$ | $$144^{\circ}$$ | $$162^{\circ}$$ |
Рішення
Сума внутрішніх кутів опуклого багатокутника дорівнює $$2d(n-2),$$ де $$d=90^{\circ},$$ $$n$$ – число вершин (сторін).
Для знаходження градусної міри внутрішнього кута правильного десятикутника загальну суму розділимо на 10.
$$\frac{2\cdot 90^{\circ}\cdot (10-2)}{10}=144^{\circ}.$$
Відповідь: Г.
Завдання 11
Спростіть вираз $$a-|a|,$$ якщо $$a <0.$$
| А | Б | В | Г | Д |
| $$2a$$ | $$a$$ | $$0$$ | $$-a$$ | $$-2a$$ |
Рішення
Оскільки $$a <0,$$ то за визначенням модуля $$|a|=-a$$
$$a-|a|=a-(-a)=2a$$
Відповідь: А.
Завдання 12
Об’єм кулі дорівнює $$36\pi$$ см3. Знайдіть її діаметр.
| А | Б | В | Г | Д |
| 3 см | 24 см | 6 см | 18 см | 12 см |
Рішення
$$V=\frac{4}{3}\pi R^3$$
$$\frac{4}{3}\pi R^3=36\pi\Rightarrow R^3=\frac{36\cdot 3}{4}=27\Rightarrow R=\sqrt[3]{27}=3\Rightarrow D=2R=6$$
Відповідь: В.
Завдання 13
Визначте знаменник геометричної прогресії $$(b_{n}),$$ якщо $$b_{9}=24, b_{6}=-\frac{1}{9}.$$
| А | Б | В | Г | Д |
| $$\frac{2}{\sqrt[3]{3}}$$ | $$-\frac{2}{\sqrt[3]{3}}$$ | $$3$$ | $$6$$ | $$-6$$ |
Рішення
$$b_{n}=b_{1}\cdot q^{n-1}$$
$$b_{9}=b_{1}\cdot q^{8}$$
$$b_{6}=b_{1}\cdot q^{5}$$
$$\left\{\begin{matrix} b_{1}\cdot q^{8}=24\\ b_{1}\cdot q^{5}=-\frac{1}{9} \end{matrix}\right.$$
Розділимо перше рівняння системи на друге
$$q^3=-24\cdot 9=-3^3\cdot 2^3\Rightarrow q=-\sqrt[3]{(2\cdot3)^3}=-6$$
Відповідь: Д.
Завдання 14
Розв’яжіть нерівність $$\frac{3x}{x+1}<\frac{7}{x+1}.$$
| А | Б | В | Г | Д |
| $$(-1;\frac{7}{3})$$ | $$(-\infty;-1)$$ | $$(-\infty;-1)\cup (\frac{7}{3};\infty)$$ | $$(-\infty;-1)\cup (-1;\frac{7}{3})$$ | $$(-\infty;\frac{7}{3})$$ |
Рішення
$$\frac{3x}{x+1}-\frac{7}{x+1}<0\Rightarrow \frac{3x-7}{x+1}<0\sim 3(x-\frac{7}{3})(x+1)<0$$
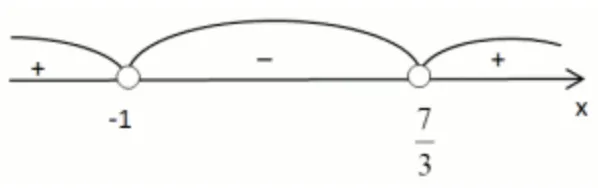
$$x\in(-1;\frac{7}{3})$$
Відповідь: А.