Завдання 1
Розв’яжіть рівняння $$\frac{2}{x}=5.$$
| А | Б | В | Г | Д |
| $$x=0.1$$ | $$x=10$$ | $$x=2.5$$ | $$x=0.4$$ | $$x=-3$$ |
Рішення
$$\frac{2}{x}=5\Rightarrow 5x=2\Rightarrow x=\frac{2}{5}=0.4$$
Відповідь: Г.
Завдання 2
Учитель роздав учням певного класу 72 зошити. Кожен учень отримав однакову кількість зошитів. Якому з поданих нижче чисел може дорівнювати кількість учнів у цьому класі?
| А | Б | В | Г | Д |
| 7 | 9 | 10 | 11 | 14 |
Рішення
Розбиваємо 72 на прості множники.
$$\begin{matrix} \left.\begin{matrix} 72\\ 36\\ 18\\ 9\\ 3\\ 1\end{matrix}\right| & \begin{matrix} 2\\ 2\\ 2\\ 3\\ 3\\ 1\end{matrix} \end{matrix}$$
$$72=2^3\cdot 3^2$$
Серед представлених варіантів підходить лише 1: 9 осіб.
Відповідь: Б.
Завдання 3
Спростіть вираз $$0.8b^9:8b^3.$$
| А | Б | В | Г | Д |
| $$0.1b^6$$ | $$10b^6$$ | $$6.4b^{12}$$ | $$0.1b^3$$ | $$10b^3$$ |
Рішення
$$0.8b^9:8b^3=\frac{8}{10}\cdot 8\cdot b^{9-3}=0.1b^6.$$
Відповідь: А.
Завдання 4
Укажіть лінійну функцію, графік якої паралельний вісі абсцис і проходить через точку $$A(-2;3).$$
| А | Б | В | Г | Д |
| $$y=\frac{3}{2}x$$ | $$y=-2$$ | $$x=-2$$ | $$x=-3$$ | $$y=3$$ |
Рішення
Оскільки графік лінійної функції $$y=ax+b$$ паралельний осі абсцис $$(Ox),$$ то $$a=0,$$ тобто отримали $$y=b.$$ Враховуючи умову проходження через точку $$A(-2;3),$$ отримуємо $$y=3.$$
Відповідь: Д.
Завдання 5
Доберіть таке закінчення речення, щоб утворилося правильне твердження: “Сума квадратів катетів прямокутного трикутника дорівнює…”.
| А | гіпотенузі |
| Б | квадрату суми катетів |
| В | квадрату гіпотенузи |
| Г | добутку катетів |
| Д | подвійному добутку катетів |
Рішення
Теорема Піфагора: У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.
Відповідь: В.
Завдання 6
Обчисліть $$\log_{2}\frac{1}{8}+\log_{5}25.$$
| А | Б | В | Г | Д |
| $$2$$ | $$-1$$ | $$5$$ | $$\lg\frac{25}{8}$$ | $$\log_{7}25\frac{1}{8}$$ |
Рішення
$$\log_{2}\frac{1}{8}+\log_{5}25=\log_{2}2^{-3}+\log_{5}5^2=-3\log_{2}2+2\log_{5}5=$$
$$=-3+2=-1$$
Відповідь: Б.
Завдання 7
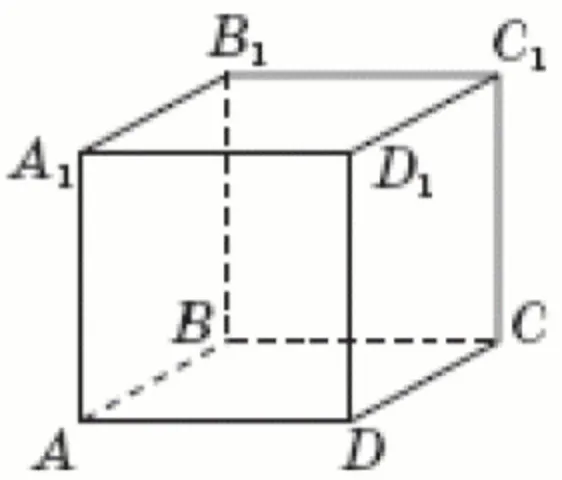
На рисунку зображено куб $$ABCDA_{1}B_{1}C_{1}D_{1}.$$ Укажіть серед поданих нижче пряму, що утворює з $$CD_1$$ пару мимобіжних прямих.
| А | Б | В | Г | Д |
| $$A_{1}B$$ | $$C_{1}D$$ | $$CB_{1}$$ | $$AB$$ | $$CD$$ |
Рішення
Серед представлених прямих тільки пряма $$AB$$ схрещується з $$CD_1.$$
Відповідь: Г.