Завдання 1
Спростіть вираз $$\frac{3x+12}{x^2-16}.$$
| А | Б | В | Г | Д |
| $$\frac{3}{4-x}$$ | $$\frac{3}{x+4}$$ | $$\frac{3}{x-4}$$ | $$-\frac{3}{x+4}$$ | $$\frac{1}{x-4}$$ |
Рішення
$$\frac{3x+12}{x^2-16}=\frac{3(x+4)}{(x-4)(x+4)}=\frac{3}{x-4}$$
Відповідь: В.
Завдання 2
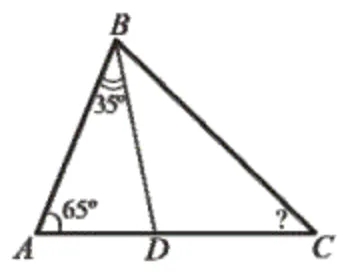
У трикутнику АВС: ∠А=65°, ВD – бісектриса кута В (див. рисунок). Знайдіть градусну міру кута ВCA, якщо ∠AВD=35°.
| А | Б | В | Г | Д |
| 35° | 45° | 50° | 55° | 65° |
Рішення
Бісектриса ділить кут В навпіл, сума кутів трикутника дорівнює $$180^{\circ},$$ значить кут ВСА дорівнює:
$$180^{\circ}-65^{\circ}-2\cdot 35^{\circ}=45^{\circ}$$
Відповідь: Б.
Завдання 3
Обчисліть $$\frac{\sqrt[3]{128}}{\sqrt[3]{2}}.$$
| А | Б | В | Г | Д |
| 64 | 18 | 8 | 4 | 2 |
Рішення
$$\frac{\sqrt[3]{128}}{\sqrt[3]{2}}=\frac{2^{\frac{7}{3}}}{2^{\frac{1}{3}}}=2^{\frac{7}{3}-\frac{1}{3}}=2^2=4$$
Відповідь: Г.
Завдання 4
Яка з поданих нижче послідовностей є арифметичною прогресією?
| А | 9; 7; 4; 1 |
| Б | -4; -2; 0; 1 |
| В | 3; 6; 12; 24 |
| Г | 1; 3; 6; 10 |
| Д | 3; 7; 11; 15 |
Рішення
$$a_{1},a_{2}, a_{3},\ldots , a_{n},\ldots$$ – арифметична прогресія
$$d=a_{2}-a_{1}=\ldots=a_{n}-a_{n-1}=\ldots$$
Цій умові задовольняє лише: 3; 7; 11; 15 (7-3=11-7=15-11=4)
Відповідь: Д.
Завдання 5
В Оксани є певна кількість горіхів. Коли вона розклала їх у купки по 5 горіхів, то два горіхи залишилися, а коли розклала їх по 3, то зайвих горіхів не виявилося. Яка кількість горіхів із запропонованих варіантів МОГЛА БУТИ в Оксани?
| А | Б | В | Г | Д |
| 32 | 45 | 57 | 63 | 81 |
Рішення
Шукане число має ділитися на 5 із залишком 2 і на 3 без залишку.
Згадаймо ознаки подільності:
Число ділиться на 3, якщо сума цифр цього числа ділиться на 3.
Число ділиться на 5, якщо його остання цифра 0 або 5.
Оскільки шукане число ділиться на 5 із залишком 2, то його остання цифра має бути або 2, або 7. Цій умові задовольняють 2 числа: 32 и 57. Сума цифр числа 32 (3+2=5) не ділиться на 3. Сума цифр числа 57 (5+7=12, 1+2=3) ділиться на 3. Отже 57 – шукане число.
Відповідь: В.
Завдання 6
Розв’яжіть нерівність $$\left ( \frac{1}{5} \right )^x\leqslant \frac{1}{25}.$$
| А | Б | В | Г | Д |
| $$(-\infty;5]$$ | $$(-\infty;2]$$ | $$(0;2]$$ | $$[2;\infty)$$ | $$[5;\infty)$$ |
Рішення
$$\left ( \frac{1}{5} \right )^x\leqslant \left (\frac{1}{5} \right )^2$$
Основа більша за нуль і менша за одиницю, знак нерівності змінюється на протилежний: $$x\geqslant 2$$
Відповідь: Г.
Завдання 7
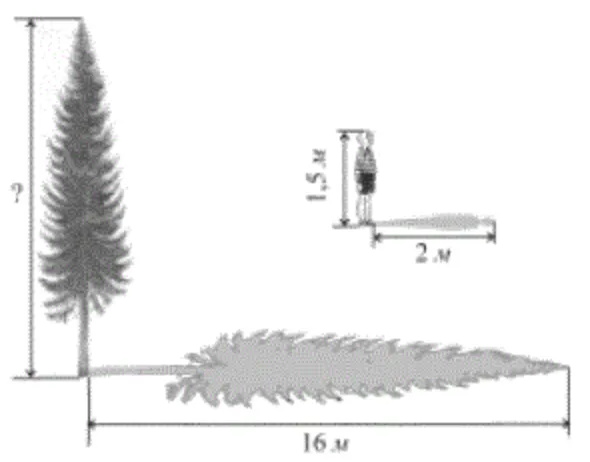
У сонячний день довжина тіні від дерева становить 16 м. У той самий час тінь від хлопчика, який має зріст 1,5 м, дорівнює 2 м (див. рисунок). Визначте висоту дерева.
| А | Б | В | Г | Д |
| 12 м | 12.5 м | 13 м | 14 м | 15.5 м |
Рішення
Складемо пропорцію: $$\frac{x}{16}=\frac{1.5}{2}$$
$$x=\frac{1.5\cdot 16}{2}=12$$
Відповідь: А.
Завдання 8
За переказ грошей клієнт повинен сплатити банку винагороду в розмірі 2% від суми переказу. Скільки всього грошей (у гривнях) йому потрібно сплатити в касу банку, якщо сума переказу становить 30 000 грн?
| А | Б | В | Г | Д |
| 36000 грн | 30600 грн | 30060 грн | 30030 грн | 30006 грн |
Рішення
$$30000\cdot2\%=600$$ – банківські послуги
$$30000+600=30600$$ – сума для оплати в касі
Відповідь: Б.