Завдання
Розв’язати нерівність: $$\log_{x^2}{\frac{2x}{x-3}}\leqslant\frac{1}{2}$$
Рішення
ОДЗ:
$$\left\{\begin{matrix}x^2>0\\ x^2\neq1\\ \frac{2x}{x-3}>0\end{matrix}\right.$$
$$\left\{\begin{matrix}x\neq0\\ x\neq\pm1\\ x(x-3)>0\end{matrix}\right.$$
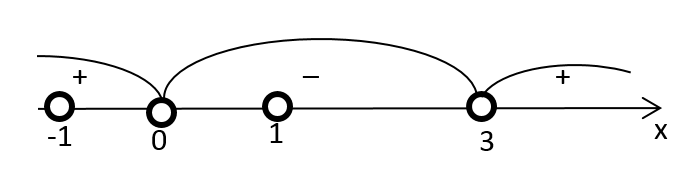
$$x\in(-\infty; -1)\cup(-1; 0)\cup(3;\infty)$$
Розв’яжемо логарифмічну нерівність
$$\log_{x^2}{\frac{2x}{x-3}}\leqslant\frac{1}{2}\log_{x^2}x^2$$
$$\log_{x^2}{\frac{2x}{x-3}}\leqslant\log_{x^2}|x|$$
Розглянемо 3 випадки
1) $$x\in(-\infty; -1)$$ – основа більша за 1, зберігаємо знак нерівності
$$\frac{2x}{x-3}\leqslant -x$$
$$\frac{2x+x^2-3x}{x-3}\leqslant 0$$
$$\frac{x(x-1)}{x-3}\leqslant 0$$

$$x\in(-\infty; 0)\cup(1;3)$$
Враховуючи інтервал, на якому розглядається рішення, отримуємо $$x\in(-\infty; -1)$$
2) $$x\in(-1;0)$$ – основа між нулем і одиницею, знак нерівності міняємо на протилежний.
$$\frac{2x}{x-3}\geqslant -x$$
$$\frac{x(x-1)}{x-3}\geqslant 0$$ (див. рисунок з пункту 1)
$$x\in(0;1)\cup(3;\infty),$$ що не потрапляє в інтервал, на якому розглядаємо розв’язок, тобто отримали порожню множину.
3) $$x\in(3;\infty)$$ – основа більша за одиницю, знак нерівності зберігаємо.
$$\frac{2x}{x-3}\leqslant x$$
$$\frac{2x-x^2+3x}{x-3}\leqslant 0$$
$$\frac{x(x-5)}{x-3}\geqslant 0$$

З урахуванням розглянутого для вирішення інтервалу, отримаємо $$x\in[5;\infty)$$
Об’єднуючи рішення трьох випадків, отримаємо $$x\in(-\infty; -1)\cup[5;\infty)$$
Відповідь: $$x\in(-\infty; -1)\cup[5;\infty)$$