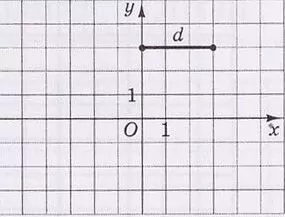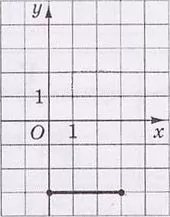Зовнішнє незалежне оцінювання 2014 з математики
Тест складається з 34 завдань різних форм і триває 150 хвилин.
Завдання оцінюються наступним чином:
За виконання тестового завдання з вибором однієї правильної відповіді (№ 1-20) можна отримати максимум 1 тестовий бал (за правильну відповідь).
За виконання тестового завдання на встановлення відповідності (логічні пари) (№ 21-24) можна отримати максимум 4 тестових бали (по 1 балу за кожну правильну логічну пару).
Завдання 25-34 – завдання відкритої форми з короткою відповіддю. Тестові завдання 25, 26 є структурними, складаються з двох частин і оцінюються максимум 2 балами (по 1 балу за правильну відповідь). За виконання тестового завдання відкритої форми з короткою відповіддю (№ 27-34) можна отримати максимум 2 тестових бали (2 бали за правильну відповідь).
Максимальна кількість тестових балів, які можна набрати, виконавши всі завдання тесту з математики, – 56.
Тест
Підсумок тесту
Завершено завдань: 0 з 34
Завдання:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
Інформація
Бажаємо успіху!
Ви вже проходили тест раніше. Ви не можете пройти його знову.
Тест завантажується...
Щоб розпочати тест, потрібно ввійти або зареєструватися.
Щоб розпочати тест, потрібно завершити наступний тест:
Результати
Правильних відповідей: 0 з 34
Ваш час:
Час вийшов
Ви набрали 0 з 0 балів, (0)
Категорії
- Не присвоєно категорію 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- З відповіддю
- Позначене
- Завдання 1 з 34
1. Завдання
Вкажіть запис числа 0.351 в стандартному вигляді.
- Завдання 2 з 34
2. Завдання
У трикутнику $$ABC$$ проведена висота $$BM$$ (див. рисунок). Визначити градусну міру кута $$MBA,$$ якщо $$\angle A=40^{\circ}.$$
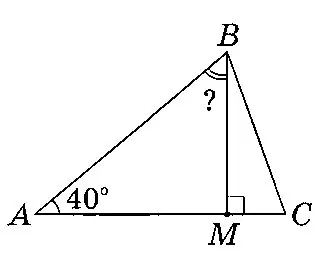
- Завдання 3 з 34
3. Завдання
Розв’язати рівняння $$\frac{x}{2}+\frac{x}{3}=2.$$
- Завдання 4 з 34
4. Завдання
Яка з наведених послідовностей є геометричною прогресією зі знаменником $$q < 0? $$
- Завдання 5 з 34
5. Завдання
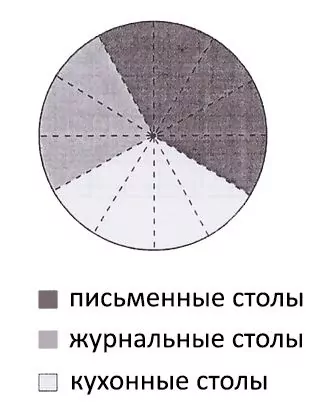
На круговій діаграмі (коло розділене пунктирними лініями на рівні сектори) показано розподіл кількості столів, проданих магазином протягом місяця (див. рисунок). Загальна кількість проданих столів за цей період склала 108. Скільки було серед них журнальних столів?

- Завдання 6 з 34
6. Завдання
Якщо число $$b$$ становить $$47\%$$ від додатного числа $$a$$, то $$b=$$
- Завдання 7 з 34
7. Завдання
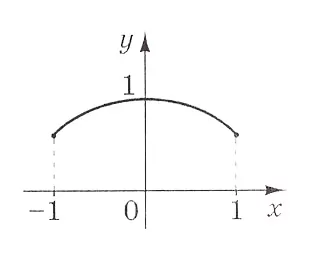
На рисунку зображено фрагмент графіка однієї з наведених функцій на відрізку $$[-1; 1].$$ Укажіть цю функцію.

- Завдання 8 з 34
8. Завдання
Укажіть проміжок, якому належить корінь рівняння $$3^x\cdot4^x=\frac{1}{144}.$$
- Завдання 9 з 34
9. Завдання
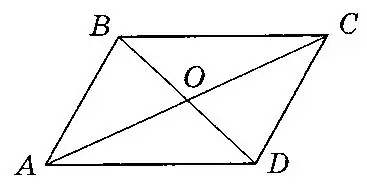
На малюнку зображено паралелограм $$ABCD,$$ діагоналі якого перетинаються в точці $$O.$$ Укажіть пару колінеарних векторів.

- Завдання 10 з 34
10. Завдання
Коло задано рівнянням $$x^2+y^2=9.$$ Визначити координати точки, що належить кругу, обмеженому цим колом.
- Завдання 11 з 34
11. Завдання
Укажіть правильну нерівність, якщо $$a=\sin 120^{\circ}, b=\cos 120^{\circ}.$$
- Завдання 12 з 34
12. Завдання
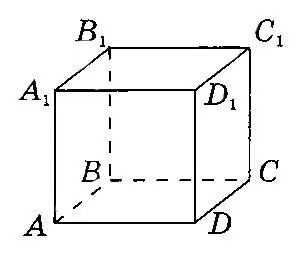
На рисунку зображено куб $$ABCDA_1B_1C_1D_1,$$ ребро якого дорівнює 1 см. Обчислити відстань від точки $$A$$ до прямої $$B_1C_1.$$

- Завдання 13 з 34
13. Завдання
Знайти всі значення $$x,$$ за яких значення виразу $$2-5x$$ належить проміжку $$(-3;6).$$
- Завдання 14 з 34
14. Завдання
Функція $$y=f(x)$$ зростає на проміжку $$(-\infty;\infty).$$ Яке з наведених чисел може бути значенням даної функції в точці $$x=8,$$ якщо $$f(1)=-2, f(9)=5?$$
- Завдання 15 з 34
15. Завдання
Довжина кола основи циліндра дорівнює $$18\pi$$ см. Визначити площу бічної поверхні цього циліндра, якщо його висота дорівнює 7 см.
- Завдання 16 з 34
16. Завдання
$$|2-\sqrt{5}|+|2+\sqrt{5}|=$$
- Завдання 17 з 34
17. Завдання
Точка $$M$$ не належить площині $$\alpha.$$ Які з наведених тверджень є правильними?
I. Через точку $$M$$ можна провести лише одну площину, паралельну площині $$\alpha.$$
II. Через точку $$M$$ можна провести лише одну площину, перпендикулярну до площини $$\alpha.$$
III. Через точку $$M$$ можна провести лише одну площину, що перетинає $$\alpha$$ під кутом $$45^{\circ}.$$
- Завдання 18 з 34
18. Завдання
Знайти похідну функції $$y=x^7\ln x.$$
- Завдання 19 з 34
19. Завдання
Об’єм конуса дорівнює 64 см3. Через середину висоти цього конуса паралельно його основі проведено площину. Отриманий переріз є основою меншого конуса, вершина якого збігається з вершиною заданого. Знайти об’єм меншого конуса.
- Завдання 20 з 34
20. Завдання
Розв’язати нерівність $$3 + \log_{2}x\geqslant0.$$
- Завдання 21 з 34
21. Завдання
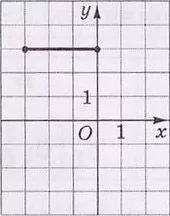
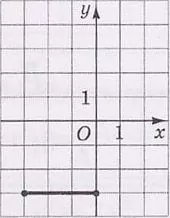
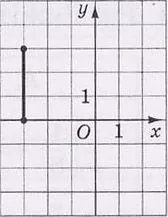
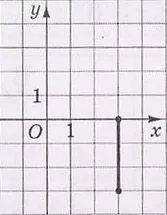
На рисунку зображено відрізок $$d$$ на координатній площині $$xy.$$ Установіть відповідність між відрізком і рисунком, на якому він зображений.

Елементи сортування
- відрізок, симетричний відрізку $$d$$ відносно осі $$x$$
- відрізок, симетричний відрізку $$d$$ відносно осі $$y$$
- відрізок, симетричний відрізку $$d$$ відносно точки $$O$$
- відрізок, у який переходить відрізок $$d$$ внаслідок повороту навколо точки $$O$$ на кут $$90^{\circ}$$ проти руху годинникової стрілки
-
- Завдання 22 з 34
22. Завдання
Установіть відповідність між заданим виразом і виразом, що тотожно дорівнює йому, якщо $$a\neq 0; a\neq 1; a\neq -1.$$
Елементи сортування
- $$a-1$$
- $$-a-1$$
- $$-\frac{1}{a+1}$$
- $$-\frac{1}{a-1}$$
- $$a+1$$
- $$\frac{a}{a+1}\cdot\frac{a^2-1}{a}$$
- $$a^2+\frac{a^3-1}{1-a}$$
- $$\frac{1-a}{a}:\frac{a^2-1}{a}$$
- $$\frac{a-2}{a-1}-1$$
- Завдання 23 з 34
23. Завдання
З усіх натуральних чисел, більших за 9 і менших за 20, навмання вибрали одне число. Установити відповідність між подією та ймовірністю її появи.
Елементи сортування
- 0.4
- 1
- 0
- 0.3
- 0.2
- вибране число буде простим
- вибране число складається з двох цифр
- вибране число буде дільником числа 5
- сума цифр обраного числа ділитиметься на 3
- Завдання 24 з 34
24. Завдання
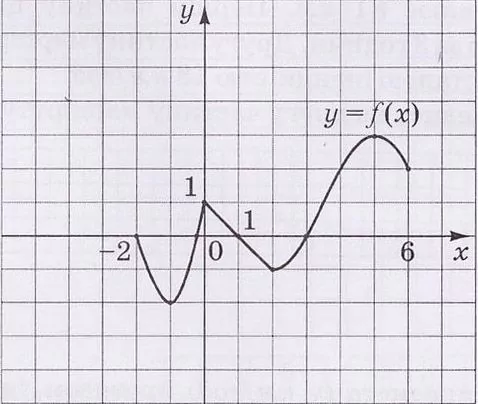
На рисунку зображено графік функції $$y=f(x),$$ визначеної на відрізку $$[-2;6].$$ Установіть відповідність між твердженнями та рівняннями прямої, для якої це твердження є правильним.

Елементи сортування
- $$y=3+x$$
- $$y=2$$
- $$y=3-x$$
- $$y=1-x$$
- $$y=1$$
- пряма не перетинає графік функції $$y=f(x)$$
- пряма є дотичною, проведеною до графіка функції $$y=f(x)$$ у точці з абсцисою $$x=5$$
- пряма перетинає графік функції $$y=f(x)$$ у точці з абсцисою $$x=3$$
- пряма має з графіком функції $$y=f(x)$$ не менше трьох спільних точок на відрізку $$[0;2]$$
- Завдання 25 з 34
25. Завдання
Довжина маршруту велосипедиста дорівнює 81 км. Першу частину цього маршруту він проїхав із постійною швидкістю за 3 години. Другу частину маршруту завдовжки 36 км велосипедист проїхав із постійною швидкістю 18 км/год.
1. Скільки часу (у годинах) витратив велосипедист на другу частину маршруту?
2. Якою була середня швидкість велосипедиста (у км/год) протягом усього маршруту?
- 1. Відповідь: (2) 2. Відповідь: (16,2, 16.2)
- Завдання 26 з 34
26. Завдання
Площа ромба дорівнює $$10.8$$ см2, а площа кола, вписаного в цей ромб – $$2.25\pi$$ см2.
1 Визначте довжину радіуса кола, вписаного в ромб (у см).
2. Обчислити довжину сторони ромба (у см).
- 1. Відповідь: (1.5, 1,5) 2. Відповідь: (3.6, 3,6)
- Завдання 27 з 34
27. Завдання
Обчислити $$\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}}5\text{ctg}x\sin x dx.$$
- Завдання 28 з 34
28. Завдання
Розв’язати нерівність $$(18+2x)^2(x^2+8x+15)\leqslant 0.$$ У відповіді запишіть суму всіх її цілих розв’язків.
- Завдання 29 з 34
29. Завдання
Обчислити значення виразу $$(\sqrt[6]{27}-\sqrt[4]{100})\cdot(\sqrt[6]{27}+\sqrt[4]{100}).$$
- Завдання 30 з 34
30. Завдання
Розв’язати систему рівнянь $$\left\{\begin{matrix}\sqrt{y-7x+33}=x\\ 4x-y=5\end{matrix}\right.$$
Якщо система має один розв’язок $$(x_0;y_0),$$ то у відповідь запишіть добуток $$x_0\cdot y_0.$$ Якщо система має два розв’язки $$(x_1;y_1)$$ та $$(x_2;y_2),$$ то у відповідь запишіть найбільший з добутків $$x_1\cdot y_1$$ та $$x_2\cdot y_2.$$
- Завдання 31 з 34
31. Завдання
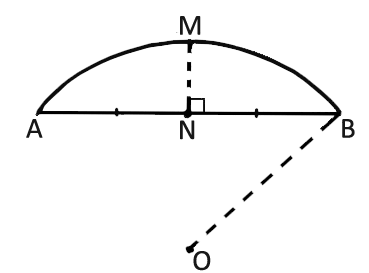
На рисунку схематично зображено опуклий міст, що має форму дуги $$AMB$$ кола з центром у точці $$O.$$ $$MN$$ – серединний перпендикуляр до $$AB,$$ $$MN=3$$ м. Визначити довжину радіуса $$OB$$ (у метрах), якщо довжина відрізка $$AB$$ дорівнює 12 м.

- Завдання 32 з 34
32. Завдання
Областю визначення періодичної функції $$y=f(x)$$ з періодом $$T=9$$ є множина всіх дійсних чисел. На проміжку $$(-5;4]$$ ця функція задана формулою $$f(x)=19-x^3.$$ Обчислити значення $$f(5).$$
- Завдання 33 з 34
33. Завдання
В основі піраміди $$SABCD$$ лежить трапеція $$ABCD$$ $$(BC\parallel AD).$$ Бічна грань $$SBC,$$ площа якої дорівнює $$24.4$$ см2, перпендикулярна до площини основи піраміди. Точка $$M$$ – середина ребра $$SB.$$ Площина $$(MAD)$$ перетинає ребро $$SC$$ у точці $$N.$$ Визначте довжину відрізка $$MN$$ (у см), якщо об’єм піраміди дорівнює $$152$$ см2, а площа її основи – $$57$$ см2.
- Завдання 34 з 34
34. Завдання
Знайти найменше значення параметра $$a,$$ за якого рівняння $$2^{\sin^2(2\pi x+\frac{5\pi}{4})}=\frac{4}{(x-a)^2-6(x-a)+13}$$ має позитивний корінь.