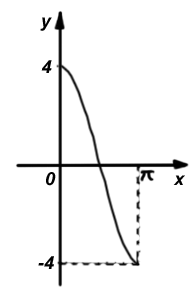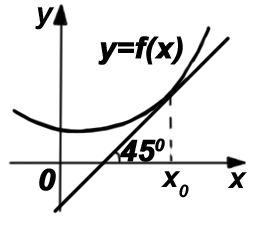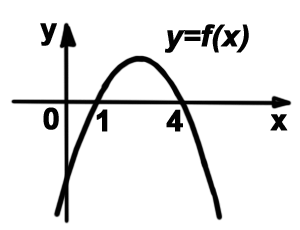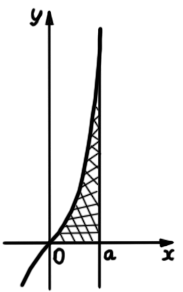Пробне зовнішнє незалежне оцінювання 2013 з математики
Пройдіть онлайн тест, щоб дізнатися, наскільки ви підготовлені до складання тестів зовнішнього незалежного оцінювання (ЗНО) з математики. Цей безплатний онлайн тест було складено на основі 33 завдань пробного ЗНО з математики від 30 березня 2013 року.
Як нараховуються бали
Завдання 1-20 оцінюються по 1 балу (за правильну відповідь), завдання 21-24 – по 4 бали (по 1 балу за кожну правильну логічну пару) і за завдання 25-33 нараховується по 2 бали (за правильну числову відповідь).
Як відповідати на тестові завдання
Для тестових завдань 1-20 виберіть правильний, на ваш погляд, варіант відповіді та натисніть кнопку Далі.
Для тестових завдань 21-24 на встановлення відповідності розташуйте (перетягніть мишкою) варіанти відповідей навпроти тверджень так, щоб утворилася правильна логічна пара і натисніть кнопку Далі.
Для тестових завдань 25-33 із числовими відповідями розглянемо на прикладах:
- Якщо у вас вийшло ціле позитивне число, наприклад 11, то в поле відповіді введіть 11 і натисніть кнопку Далі.;
- Якщо у вас вийшло ціле від’ємне число, наприклад -8, то в поле відповіді введіть -8 і натисніть Далі;
- Якщо у вас вийшло дробове додатне число, наприклад 5.004, то в поле відповіді введіть 5.004 (використовуйте крапку) і натисніть кнопку Далі;
- Якщо у вас вийшло дробове від’ємне число, наприклад -2.6, то в поле відповіді введіть -2.6 (використовуйте крапку) і натисніть кнопку Далі.
Тривалість тесту
Тест триває 2 години 30 хвилин. Не поспішайте. Для переходу до потрібного завдання Ви можете скористатися блоком навігації вгорі тесту.
Увага! Тест буде завершено автоматично після закінчення відведеного часу.
Тест
Підсумок тесту
Завершено завдань: 0 з 33
Завдання:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
Інформація
Бажаємо успіху!
Ви вже проходили тест раніше. Ви не можете пройти його знову.
Тест завантажується...
Щоб розпочати тест, потрібно ввійти або зареєструватися.
Щоб розпочати тест, потрібно завершити наступний тест:
Результати
Правильних відповідей: 0 з 33
Ваш час:
Час вийшов
Ви набрали 0 з 0 балів, (0)
Категорії
- Не присвоєно категорію 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- З відповіддю
- Позначене
- Завдання 1 з 33
1. Завдання
Кількість балів: 1Розташуйте в порядку зростання числа $$\frac{1}{9};\,0.1;\,0.11.$$
Правильно
Неправильно
- Завдання 2 з 33
2. Завдання
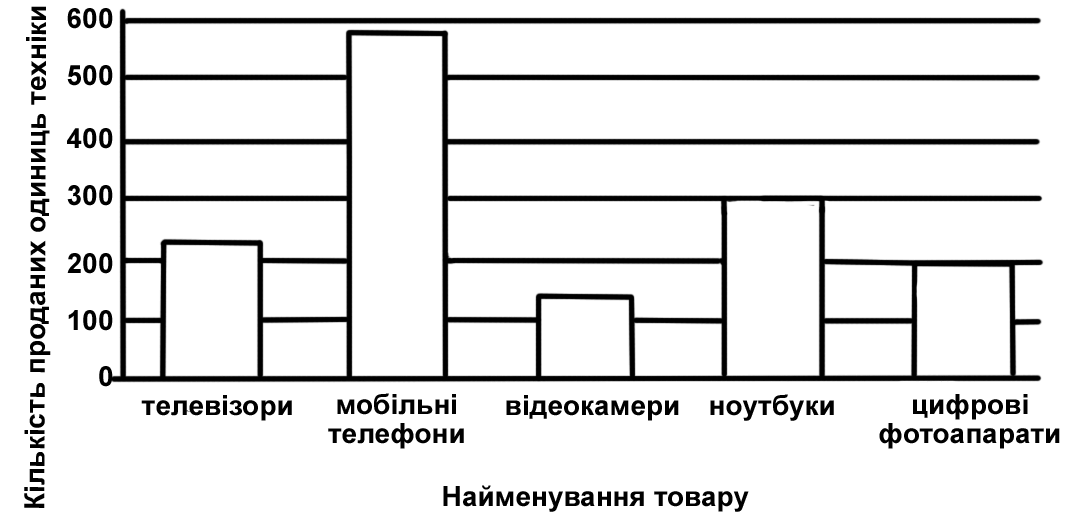
Кількість балів: 1Діаграма, зображена на рисунку, містить інформацію про кількість проданих одиниць техніки в супермаркеті електроніки протягом одного кварталу.
Використовуючи дані діаграми, доберіть таке закінчення речення, щоб утворилося правильне твердження: “Більше ніж цифрових фотоапаратів, але менше ніж мобільних телефонів, у цьому супермаркеті продано…”.
 Правильно
Правильно
Неправильно
- Завдання 3 з 33
3. Завдання
Кількість балів: 1Точки B і C лежать на прямій, що паралельна прямій a. Скільки існує площин, які паралельні прямій a і проходять через точки B і C?
Правильно
Неправильно
- Завдання 4 з 33
4. Завдання
Кількість балів: 1На рисунку зображено графік функції $$y=f(x)$$, яка визначена на відрізку $$[-4;3].$$ Укажіть область значень цієї функції.
 Правильно
Правильно
Неправильно
- Завдання 5 з 33
5. Завдання
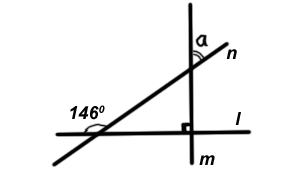
Кількість балів: 1Пряма $$n$$ перетинає перпендикулярні прямі $$l$$ і $$m$$ (див. рисунок). Визначте градусну міру кута $$a$$.
 Правильно
Правильно
Неправильно
- Завдання 6 з 33
6. Завдання
Кількість балів: 1Розв’яжіть рівняння $$\frac{2x-3}{3}=\frac{x+1}{6}.$$
Правильно
Неправильно
- Завдання 7 з 33
7. Завдання
Кількість балів: 1Діагоналі паралелограма $$ABCD$$ перетинаються в точці $$O$$ (див. рисунок). Укажіть правильну векторну рівність.
 Правильно
Правильно
Неправильно
- Завдання 8 з 33
8. Завдання
Кількість балів: 1Розв’яжіть нерівність $$2x\geqslant x^2.$$
Правильно
Неправильно
- Завдання 9 з 33
9. Завдання
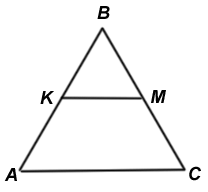
Кількість балів: 1На рисунку зображено рівносторонній трикутник $$ABC,$$ $$KM$$ – його середня лінія. Периметр трикутника $$KBM$$ дорівнює 12 см. Визначте периметр чотирикутника $$AKMC.$$
 Правильно
Правильно
Неправильно
- Завдання 10 з 33
10. Завдання
Кількість балів: 1Обчисліть $$\sqrt{2}\cdot\sqrt{0.08}.$$
Правильно
Неправильно
- Завдання 11 з 33
11. Завдання
Кількість балів: 1На рисунку зображено фрагмент графіка однієї з наведених функцій на відрізку $$[0;\pi].$$ Укажіть цю функцію.
 Правильно
Правильно
Неправильно
- Завдання 12 з 33
12. Завдання
Кількість балів: 1У першому ряду кінотеатру встановлено 15 крісел, а у кожному наступному – на 3 крісла більше, ніж у попередньому. Скільки всього крісел встановлено в сьомому ряду цього кінотеатру?
Правильно
Неправильно
- Завдання 13 з 33
13. Завдання
Кількість балів: 1Спростіть вираз $$\frac{9-x^2}{x^2+6x+9}.$$
Правильно
Неправильно
- Завдання 14 з 33
14. Завдання
Кількість балів: 1Діаметр основи конуса дорівнює 6 см, а площа його бічної поверхні – $$24\pi$$ см2. Знайдіть довжину твірної конуса.
Правильно
Неправильно
- Завдання 15 з 33
15. Завдання
Кількість балів: 1На рисунку зображено круг з центром у точці О, радіус якого дорівнює 12 см. Радіуси ОА та ОВ ділять круг на два кругові сектори. Визначте площу більшого сектора, якщо кут $$\alpha=120^{\circ}.$$
 Правильно
Правильно
Неправильно
- Завдання 16 з 33
16. Завдання
Кількість балів: 1Апофема правильної чотирикутної піраміди дорівнює 10 см, її висота – 8 см. Знайдіть довжину сторони основи піраміди.
Правильно
Неправильно
- Завдання 17 з 33
17. Завдання
Кількість балів: 1Спростіть вираз $$(1+\text{tg}^2\alpha)\cdot\sin^2\alpha.$$
Правильно
Неправильно
- Завдання 18 з 33
18. Завдання
Кількість балів: 1Дотична, проведена до графіка функції $$y=f(x)$$ в точці з абсцисою $$x_0,$$ нахилена до додатного напряму осі $$Ox$$ під кутом $$45^{\circ}$$ (див. рисунок). Знайдіть $$f'(x_0).$$
 Правильно
Правильно
Неправильно
- Завдання 19 з 33
19. Завдання
Кількість балів: 1Укажіть найменший додатний корінь рівняння $$\sin\left ( x+\frac{\pi}{3} \right )=0.$$
Правильно
Неправильно
- Завдання 20 з 33
20. Завдання
Кількість балів: 1На рисунку зображено графік квадратичної функції $$y=f(x),$$ який перетинає вісь $$Ox$$ в точках $$(1;0)$$ та $$(4;0).$$ Знайдіть множину всіх розв’язків нерівності $$x\cdot f(x)<0.$$
 Правильно
Правильно
Неправильно
- Завдання 21 з 33
21. Завдання
Кількість балів: 4У лабораторії є два сплави міді з оловом: перший масою 50 кг містить 10% міді, другий масою 100 кг містить 25% міді. Доберіть до кожного запитання правильну відповідь.
Елементи сортування
- 5
- 30
- 20
- 25
- 15
- Скільки кілограмів міді міститься у першому сплаві?
- Скільки кілограмів міді міститься у двох сплавах разом?
- Якщо із даних сплавів утворити новий сплав, то скільки відсотків міді міститиме цей сплав?
- Скільки кілограмів другого сплаву треба додати до першого, щоб утворити сплав, який міститиме 15% міді?
Правильно
Неправильно
- Завдання 22 з 33
22. Завдання
Кількість балів: 4Кожній функції поставте у відповідність координатні чверті, у яких розміщено графік цієї функції.
Елементи сортування
- лише І, ІІ та ІІІ
- лише І та ІІІ
- лише І та ІІ
- I, ІІ, ІІІ та IV
- лише І, ІІІ та IV
- $$y=x+1$$
- $$y=\frac{1}{x}$$
- $$y=2^x$$
- $$y=x^2-1$$
Правильно
Неправильно
- Завдання 23 з 33
23. Завдання
Кількість балів: 4У прямокутній системі координат у просторі зображено прямокутний паралелепіпед $$ABCDA_1B_1C_1D_1,$$ ребра $$AB,BC,BB_1$$ якого лежать на координатних осях (див. рисунок). Вершина $$D_1$$ має координати $$(4;8;12).$$ До кожного початку речення доберіть його закінчення так, щоб утворилося правильне твердження.

Елементи сортування
- збігається з точкою $$B_1.$$
- належить ребру $$CD.$$
- належить грані $$AA_1D_1D.$$
- належить діагоналі $$BC_1.$$
- належить діагоналі $$AC_1.$$
- Точка $$K(0;0;12)$$
- Точка $$M(1;8;0)$$
- Точка $$P(4;4;4)$$
- Точка $$Q(0;4;6)$$
Правильно
Неправильно
- Завдання 24 з 33
24. Завдання
Кількість балів: 4Установіть відповідність між многокутником і радіусом кола, вписаного в цей многокутник.
Елементи сортування
- 1.5 см
- 1 см
- 2 см
- $$\sqrt{3}$$ см
- 4 см
- рівносторонній трикутник зі стороною $$3\sqrt{3}$$ см
- квадрат зі стороною 2 см
- прямокутний трикутник із катетами 6 см і 8 см
- правильний шестикутник зі стороною 2 см
Правильно
Неправильно
- Завдання 25 з 33
25. Завдання
Кількість балів: 2При кожному пострілі в мішень спортсмен влучав або в “десятку”, або в “дев’ятку”, за що йому нарахувалося 10 або 9 очок відповідно. За 10 пострілів він набрав 94 очки. Скільки разів з цих 10 пострілів спортсмен влучив у “дев’ятку”?
Правильно
Неправильно
- Завдання 26 з 33
26. Завдання
Кількість балів: 2При якому значенні $$x$$ функція $$y=4-|20x+7|$$ набуває найбільшого значення?
Правильно
Неправильно
- Завдання 27 з 33
27. Завдання
Кількість балів: 2Розв’яжіть систему нерівностей $$\left\{\begin{matrix} (0.5)^{1-2x} & > & (0.5)^{8+x}\\ \frac{4}{x-5}&< &0 \end{matrix}\right..$$
У відповідь запишіть кількість усіх цілих розв’язків цієї системи. Якщо система має безліч цілих розв’язків, то у відповіді запишіть число 100.
Правильно
Неправильно
- Завдання 28 з 33
28. Завдання
Кількість балів: 2Обчисліть $$\log_{b}a,$$ якщо $$\log_{3}a=8,\,\log_{3}b=5.$$
Правильно
Неправильно
- Завдання 29 з 33
29. Завдання
Кількість балів: 2Студенти двох груп (у першій – 20 студентів, у другій – 25 студентів) обирають по одному представнику з кожної групи для участі в студентському заході. Знайдіть ймовірність того, що учасниками заходу будуть обрані старости цих груп. Вважайте, що всі студенти кожної групи мають однакові шанси стати учасниками заходу, і в кожній групі є один староста.
Правильно
Неправильно
- Завдання 30 з 33
30. Завдання
Кількість балів: 2У прямокутній трапеції $$ABCD\;(AD\parallel BC)$$ діагональ $$AC$$ перпендикулярна до бічної сторони $$CD.$$ Знайдіть довжину цієї діагоналі (у см), якщо $$AD=18$$ см, $$BC=8$$ см.
Правильно
Неправильно
- Завдання 31 з 33
31. Завдання
Кількість балів: 2У прямокутній системі координат зображено ескіз графіка функції $$y=\frac{x^3}{2}+x$$ і пряму, задану рівнянням $$x=a$$ (див. рисунок). При якому додатному значенні $$a$$ площа заштрихованої фігури дорівнюватиме 40 кв. од.?
 Правильно
Правильно
Неправильно
- Завдання 32 з 33
32. Завдання
Кількість балів: 2Основою прямої призми $$ABCDA_1B_1C_1D_1$$ є ромб $$ABCD,$$ у якому більша діагональ $$AC=17$$ см. Об’єм призми дорівнює 1020 см3. Через діагональ $$AC$$ та вершину $$B_1$$ тупого кута верхньої основи призми проведено площину, яка утворює з площиною основи кут $$\alpha.$$ Знайдіть площу утвореного перерізу призми (у см2), якщо $$\text{tg}\,\alpha=2.4.$$
Правильно
Неправильно
- Завдання 33 з 33
33. Завдання
Кількість балів: 2Знайдіть найменше ціле значення параметра $$a,$$ при якому рівняння $$\sqrt{x^2-5x}+\sqrt{x^2-9x+20}=\sqrt{a}\cdot\sqrt{x-5}$$ має два корені.
Правильно
Неправильно