Завдання 17
Розв’яжіть рівняння $$2\sin x=1.$$
| А | $$\pm \frac{\pi}{6}+2\pi n, n\in \mathbb{Z}$$ |
| Б | $$(-1)^n \cdot\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$ |
| В | $$(-1)^n \cdot\frac{\pi}{6}+2\pi n, n\in \mathbb{Z}$$ |
| Г | $$\pm \frac{\pi}{3}+2\pi n, n\in \mathbb{Z}$$ |
| Д | $$(-1)^n \cdot\frac{\pi}{6}+\pi n, n\in \mathbb{Z}$$ |
Рішення
$$\sin x=\frac{1}{2}$$ – найпростіше тригонометричне рівняння
$$x=(-1)^n arcsin\frac{1}{2}+\pi n, n\in \mathbb{Z}$$
$$x=(-1)^n \cdot\frac{\pi}{6}+\pi n, n\in \mathbb{Z}$$
Відповідь: Д.
Завдання 18
До складу української Прем’єр-ліги з футболу входять 16 команд. Упродовж сезону кожні дві команди грають між собою 2 матчі. Скільки всього матчів буде зіграно за сезон?
| А | Б | В | Г | Д |
| 120 | 128 | 200 | 240 | 256 |
Рішення
Ймовірнісна задача на розміщення.
$$A_{n}^k=\frac{n!}{(n-k)!}$$ – кількість розміщень із n по k.
$$A_{16}^2=\frac{16!}{(16-2)!}=\frac{16!}{14!}=\frac{16\cdot15\cdot14!}{14!}=16\cdot15=240$$
Відповідь: Г.
Завдання 19
Гострий кут паралелограма дорівнює $$60^{\circ},$$ а його сторони – 3 см і 4 см. Обчисліть довжину меншої діагоналі паралелограма.
| А | Б | В | Г | Д |
| $$\sqrt{37}$$ см | $$\sqrt{31}$$ см | 5 см | $$\sqrt{19}$$ см | $$\sqrt{13}$$ см |
Рішення
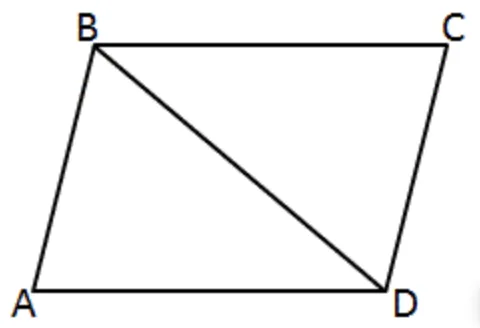
ABCD – паралелограм. AB=DC=3 см, AD=BC=4 см, BD – менша діагональ паралелограма. $$\angle A=60^{\circ}.$$ Розглянемо трикутник ABD.
За теоремою косинусів:
$$BD^2=AB^2+AD^2-2AB\cdot AD\cdot \cos\angle A$$
$$BD^2=3^2+4^2-2\cdot3\cdot 4\cdot \cos60^{\circ}=9+16-24\cdot\frac{1}{2}=13$$
$$BD=\sqrt{13}$$
Відповідь: Д.
Завдання 20
Свинцеву кулю радіуса 5 см перетопили в кульки однакового розміру, радіус кожної з яких – 1 см. Скільки таких кульок одержали? Втратами свинцю під час перетоплення знехтуйте.
| А | Б | В | Г | Д |
| 125 | 50 | 25 | 10 | 5 |
Рішення
$$V=\frac{4}{3}\pi R^3$$ – об’єм вихідної кулі, $$V_{1}=\frac{4}{3}\pi r^3$$ – об’єм отриманої кулі. $$R=5, r=1.$$
Для знаходження кількості знайдемо відношення об’ємів вихідної кулі до отриманої: $$\frac{V}{V_{1}}=\frac{\frac{4}{3}\pi R^3}{\frac{4}{3}\pi r^3}=\frac{R^3}{r^3}=\frac{5^3}{1^3}=125$$
Відповідь: А.
Завдання 21
Обчисліть $$\frac{2^{-1.6}\cdot 4^{4.8}}{8^{\frac{2}{3}}}.$$
Рішення
$$\frac{2^{-1.6}\cdot 4^{4.8}}{8^{\frac{2}{3}}}=\frac{2^{-1.6}\cdot (2^2)^{4.8}}{(2^3)^{\frac{2}{3}}}=\frac{2^{-1.6}\cdot 2^{9.6}}{2^2}=2^{-1.6+9.6-2}=2^6=64$$
Відповідь: 64.
Завдання 22
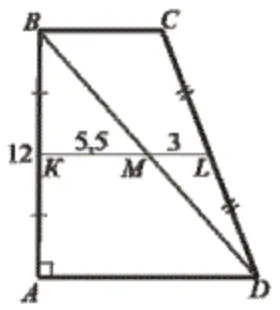
У трапеції ABCD : $$\angle A=90^{\circ}$$ AB=12 см (див. рисунок). Діагональ BD ділить середню лінію KL трапеції на відрізки KM і ML, причому KM=5,5 см і ML = 3 см. Обчисліть периметр трапеції ABCD (у см).
Рішення
$$KL=\frac{AD+BC}{2}, KL=KM+ML=5.5+3=8.5\Rightarrow AD+BC=17$$ см
$$\triangle ABD\sim \triangle KBM\Rightarrow \frac{AB}{KB}=\frac{AD}{KM}\Rightarrow AD=\frac{AB\cdot KM}{KB}=\frac{12\cdot 5.5}{6}=11$$ см
$$BC=17-AD=17-11=6$$ см
З точки $$C$$ опустимо висоту на $$AD.$$ Отримаємо прямокутний трикутник зі сторонами, що дорівнюють $$AB=12$$ см, $$AD-BC=11-6=5$$ см та $$CD$$. За теоремою Піфагора знаходимо $$CD=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13$$ см.
$$P=AB+BC+CD+AD=12+6+13+11=42$$ см.
Відповідь: 42.
Завдання 23
Обчисліть $$\cos \alpha,$$ якщо $$\sin \alpha=0.8$$ і $$\frac{\pi}{2}<\alpha<\pi.$$
Рішення
Оскільки $$\frac{\pi}{2}<\alpha<\pi,$$ то кут у другій чверті, де $$\cos \alpha$$ набуває від’ємних значень. З основної тригонометричної тотожності
$$\cos \alpha=-\sqrt{1-\sin^2 \alpha}=-\sqrt{1-0.64}=-\sqrt{0.36}=-0.6$$
Відповідь: $$-0.6.$$
Завдання 24
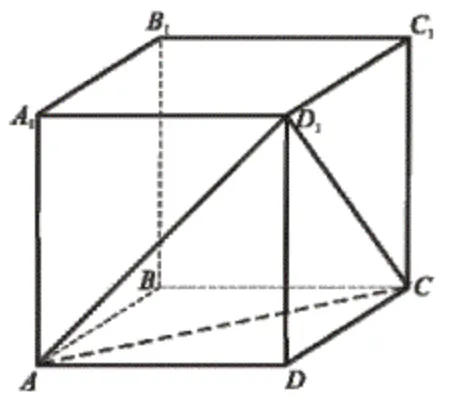
Об’єм куба $$ABCDA_{1}B_{1}C_{1}D_{1}$$ дорівнює 216 см3 (див. рисунок). Обчисліть об’єм піраміди $$D_{1}ACD$$ (у см3).
Рішення
$$V_{ABCDA_{1}B_{1}C_{1}D_{1}}=a\cdot b\cdot c$$ – об’єм кулі, $$a=AD, b=DC, c=D_{1}B$$
$$V_{D_{1}ACD}=\frac{1}{3}SH, S=\frac{1}{2}\cdot a\cdot b, H=c\Rightarrow V_{D_{1}ACD}=\frac{1}{3}\cdot \frac{1}{2}\cdot a\cdot b\cdot c=\frac{1}{6}\cdot a\cdot b\cdot c$$
$$V_{D_{1}ACD}=\frac{V_{ABCDA_{1}B_{1}C_{1}D_{1}}}{6}=\frac{216}{6}=36$$
Відповідь: 36.