Завдання 7
Укажіть правильну нерівність, якщо $$a=5\sqrt{2}, b=7, c=\sqrt{51}$$
| А | Б | В | Г | Д |
| $$b<a<c$$ | $$a<b<c$$ | $$c<a<b$$ | $$a<c<b$$ | $$b<c<a$$ |
Рішення
$$a=5\sqrt{2}=\sqrt{50}, b=7=\sqrt{49}, c=\sqrt{51}$$
$$49<50<51\Rightarrow \sqrt{49}<\sqrt{50}<\sqrt{51}\Rightarrow b<a<c$$
Відповідь: А.
Завдання 8
Знайдіть значення виразу $$\cos^4\frac{\pi}{12}-\sin^4\frac{\pi}{12}$$
| А | Б | В | Г | Д |
| $$1$$ | $$\frac{\sqrt{3}}{2}$$ | $$\frac{1}{2}$$ | $$\frac{\sqrt{2}}{2}$$ | інша відповідь |
Рішення
$$\cos^4\frac{\pi}{12}-\sin^4\frac{\pi}{12}=(\cos^2\frac{\pi}{12}-\sin^2\frac{\pi}{12})(\cos^2\frac{\pi}{12}+\sin^2\frac{\pi}{12})=\cos \frac{\pi}{6}\cdot1=\frac{\sqrt{3}}{2}$$
Відповідь: Б.
Завдання 9
Знайдіть найменший додатний період функції $$y=2\cdot ctg 3x$$
| А | Б | В | Г | Д |
| $$2\pi$$ | $$\pi$$ | $$\frac{\pi}{3}$$ | $$\frac{2\pi}{3}$$ | $$\frac{\pi}{2}$$ |
Рішення
$$ctg(x+k\pi)=ctg x, k\in \mathbb{Z}, \pi$$ – найменший додатний період функції $$ctg x$$.
$$ctg 3x=ctg(3x+k\pi)=ctg 3(x+\frac{k\pi}{3}), k\in \mathbb{Z}, \frac{\pi}{3}$$ – найменший додатний період функції $$y=2\cdot ctg 3x$$.
Відповідь: В.
Завдання 10
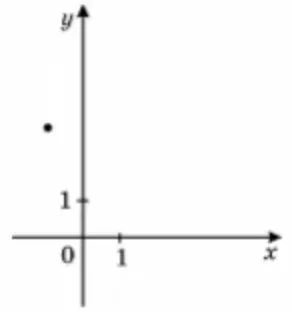
На рисунку зображено точку, через яку проходить графік функції $$y=f(x)$$. Укажіть функцію $$f(x)$$.
| А | Б | В | Г | Д |
| $$f(x)=-x$$ | $$f(x)=\sqrt{x}$$ | $$f(x)=\log_{2}x$$ | $$f(x)=x^3$$ | $$f(x)=3^{-x}$$ |
Рішення
З графіка видно, що точка лежить у II півплощині, тобто. $$x$$ набуває від’ємного значення, а $$y$$ – позитивного.
$$f(x)=\sqrt{x}$$, $$f(x)=\log_{2}x$$ не підходять, тому що для цих функцій $$x$$ не може бути негативним.
$$f(x)=x^3$$ не підходить, оскільки ця функція є непарною і від’ємному значенню змінної має відповідати від’ємне значення функції.
$$f(x)=-x$$ не підходить, тому що функція повинна приймати значення змінної з протилежним знаком (з графіка видно, що значення функції в кілька разів більше).
Залишається функція $$f(x)=3^{-x}=\frac{1}{3^x}=\left (\frac{1}{3} \right )^x$$ – спадна функція (показникова функція з основою між нулем і одиницею), яка і є відповіддю (наприклад, $$x=-1\Rightarrow y=3$$).
Відповідь: Д.
Завдання 11
Розв’яжіть рівняння $$\sin x-\sqrt{3}\cos x=0$$
| А | Б | В | Г | Д |
| $$-\frac{\pi}{6}+\pi n, n\in \mathbb{Z}$$ | $$-\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$ | $$\frac{\pi}{6}+\pi n, n\in \mathbb{Z}$$ | $$\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$ | $$\frac{\pi}{2}+\pi n, n\in \mathbb{Z}$$ |
Рішення
Згадаймо формулу:
$$a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\phi), tg\phi=\frac{b}{a}$$
У нашому випадку:
$$a=1, b=-\sqrt{3}\Rightarrow \sin x-\sqrt{3}\cos x=\sqrt{1^2+(-\sqrt{3})^2}\sin(x+\phi)$$
$$tg\phi=-\sqrt{3}\Rightarrow \phi=arctg(-\sqrt{3})=-\frac{\pi}{3}$$
Отже, $$\sin x-\sqrt{3}\cos x=2\sin(x-\frac{\pi}{3})$$
Отримали рівняння:
$$2\sin(x-\frac{\pi}{3})=0$$
$$\sin(x-\frac{\pi}{3})=0$$
Згадаймо формулу (окремий випадок):
$$\sin x=0\Rightarrow x=\pi n, n\in \mathbb{Z}$$
У нашому випадку:
$$x-\frac{\pi}{3}=\pi n, n\in \mathbb{Z}\Rightarrow x=\frac{\pi}{3}+\pi n, n\in \mathbb{Z}$$
Відповідь: Г.
Завдання 12
Обчисліть $$\log_{a}\sqrt{ab}$$, якщо $$\log_{a}b=7$$
| А | Б | В | Г | Д |
| $$\frac{2}{3}$$ | $$2$$ | $$3$$ | $$\frac{7}{2}$$ | $$4$$ |
Рішення
$$\log_{a}\sqrt{ab}=\log_{a}\left (ab \right )^\frac{1}{2}=\frac{1}{2}\log_{a}ab=\frac{1}{2}\cdot\left (\log_{a}a+\log_{a}b \right )=\frac{1}{2}\cdot\left ( 1+7 \right )=4$$
Відповідь: Д.