Завдання 1
Знайдіть натуральне, одноцифрове число N, якщо відомо, що сума 510+N ділиться на 9 без остачі.
| А | Б | В | Г | Д |
| 1 | 3 | 5 | 6 | 9 |
Рішення
Число ділиться на 9 тоді й тільки тоді, коли сума його цифр ділиться на 9.
Число N одноцифрове (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
Знайдемо суму цифр числа 510+N=5+1+N=6+N
Очевидно, що шукане число N=3, бо 6+3=9 ділиться на 9
Відповідь: Б.
Завдання 2
Визначте кількість усіх дробів зі знаменником 28, які більші за $$\frac{4}{7},$$ але менші від $$\frac{3}{4}.$$
| А | Б | В | Г | Д |
| шість | чотири | три | два | один |
Рішення
$$\frac{4}{7}=\frac{16}{28}<\frac{x}{28}<\frac{3}{4}=\frac{21}{28}$$
$$\frac{17}{28};\frac{18}{28};\frac{19}{28};\frac{20}{28}$$ – чотири шукані дроби.
Відповідь: Б
Завдання 3
Під час закладання нового парку 25% його площі відвели під посадку кленів, 50% площі, що залишилася, ⎯ під посадку дубів, а решту площі ⎯ під газони. Вкажіть, на якій із діаграм правильно показано розподіл посадок.
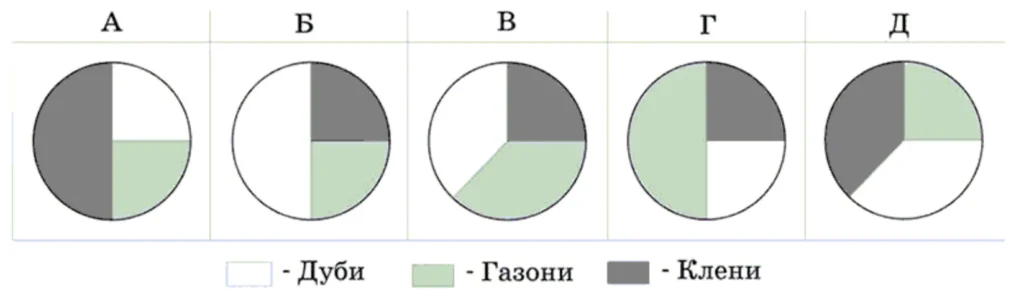
Рішення
Під посадку кленів відвели 25% усієї площі – це $$\frac{1}{4}$$ (або Б, або В, або Г).
Отже, залишилося 75% від усієї площі, тобто $$\frac{3}{4}.$$
За умовою 50% від площі, що залишилася (від $$\frac{3}{4})$$ відвели під дуби. Отже, нам потрібно розподілити порівну частину, що залишилася, для дубів і газонів $$(\frac{3}{4}\cdot\frac{1}{2}=\frac{3}{8}$$ від усієї площі). Такому розподілу відповідає лише В.
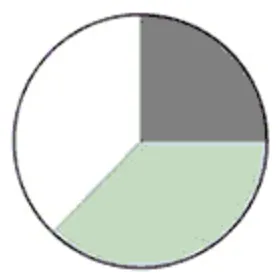
Відповідь: В
Завдання 4
Розв’яжіть нерівність $$\frac{x^2+64}{x-5}>0.$$
| А | Б | В | Г | Д |
| $$(-\infty;5)\cup (8;\infty)$$ | $$(-\infty;5)\cup (5;\infty)$$ | $$(5;8)$$ | $$(5;\infty)$$ | $$(-\infty;5)$$ |
Рішення
$$x^2+64>0$$ $$\Rightarrow x-5>0$$ $$\Rightarrow x>5$$
Відповідь: Г
Завдання 5
Якщо $$F=\frac{GMm}{R^2}$$ і $$R>0,$$ то $$R=$$
| А | Б | В | Г | Д |
| $$\sqrt{FGMm}$$ | $$\sqrt{\frac{Mm}{GF}}$$ | $$\sqrt{\frac{GF}{Mm}}$$ | $$\sqrt{\frac{F}{GMm}}$$ | $$\sqrt{\frac{GMm}{F}}$$ |
Рішення
$$F=\frac{GMm}{R^2}$$ $$\Rightarrow R^2=\frac{GMm}{F}$$ $$\Rightarrow R=\sqrt{\frac{GMm}{F}}$$
Відповідь: Д
Завдання 6
В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду (мода − це те значення випадкової величини, яке зустрічається найчастіше) даного розподілу за допомогою зображеного на рисунку полігона частот.
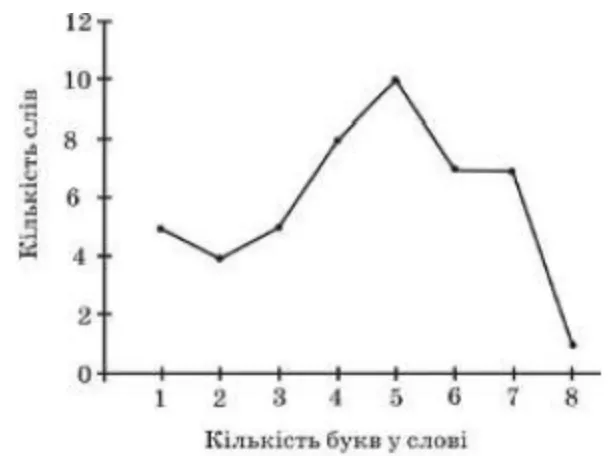
| А | Б | В | Г | Д |
| 2 | 4 | 5 | 8 | 10 |
Рішення
З полігона частот, зображеного на рисунку, видно, що найчастіше трапляються слова (10 слів), які складаються з п’яти літер, отже, мода дорівнює 5.
Відповідь: В