Завдання
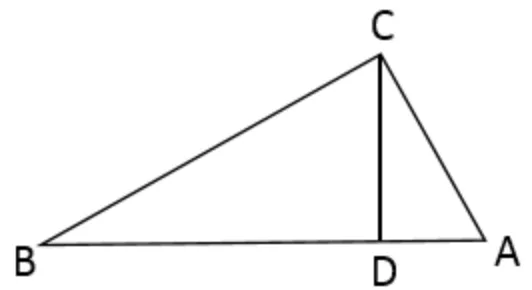
Катети прямокутного трикутника відносяться як 3:4, а гіпотенуза дорівнює 5 см. Знайдіть відрізки, на які висота, проведена з вершини прямого кута, ділить гіпотенузу.
Рішення
$$ABC$$ – прямокутний трикутник: $$\angle C=90^{\circ}$$, $$\frac{AC}{BC}=\frac{4}{3}$$, $$AB=5$$ см, $$CD$$ – висота.
Нехай $$x$$ – коефіцієнт пропорційності, тоді $$AC=3x$$ см, $$BC=4x$$ см. За теоремою Піфагора $$AB^2=BC^2+AC^2$$
$$25=(4x)^2+(3x)^2$$
$$25=25x^2$$
$$x^2=1$$
Прямокутний трикутник $$ADC$$ подібний прямокутному трикутнику $$ABC$$ (по гострому куту). З подібності трикутників випливає: $$\frac{AC}{AD}=\frac{BC}{CD}=\frac{AB}{AC}$$
Розглянемо $$\frac{AC}{AD}=\frac{AB}{AC}$$, підставимо в пропорцію відомі значення:
$$\frac{3x}{AD}=\frac{5}{3x}\Rightarrow AD=\frac{9x^2}{5}$$
$$AD=\frac{9}{5}=1.8$$ (см)
$$BD=AB-AD=5-1.8=3.2$$ (см)
Відповідь: 1.8 см; 3.2 см.