Розглянемо геометричне завдання на відповідність логічних пар, взяте з посібника “Математика: Комплексна підготовка до зовнішнього незалежного оцінювання”, але без друкарської помилки, присутній у посібнику.
Завдання
Дві площини, що перетинаються під кутом 60°, торкаються сфери. Установити відповідність між площею сфери (1-4) і відстанню від центру сфери до лінії перетину площин (А-Д).
| 1 | $$36\pi$$ см2 | А | $$8\sqrt{3}$$ см |
| 2 | $$12\pi$$ см2 | Б | $$6$$ см |
| 3 | $$48\pi$$ см2 | В | $$2\sqrt{3}$$ см |
| 4 | $$192\pi$$ см2 | Г | $$5\sqrt{3}$$ см |
| Д | $$4\sqrt{3}$$ см |
Рішення
Дана сфера з центром у точці $$O$$ та радіусом $$R$$. Площини $$\alpha$$ та $$\beta$$ торкаються сфери відповідно в точках $$A$$ та $$B$$ (кожна площина лише в 1 точці).
Проведемо площину через точки $$O,A,B$$. Позначимо точку отриманої площини, що належить до лінії перетину площин $$\alpha$$ і $$\beta$$ точкою $$C$$. Перейдемо до завдання на площині.
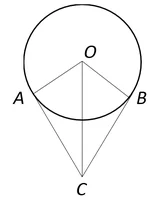
Пригадаємо визначення та властивості дотичної до окружності.
Визначення: Пряма, що має з окружністю тільки одну спільну точку, називається дотичною до окружності, а їхня спільна точка називається точкою дотику прямої та окружності.
Властивості:
1. Дотична до окружності перпендикулярна радіусу, проведеному в точку торкання.
2. Відрізки дотичних до окружності, проведених з однієї точки, рівні та становлять однакові кути з прямою, що проходить через цю точку та центр окружності.
За умовою $$\angle ACB=60^{\circ}$$. $$AC$$ та $$BC$$ – дотичні до окружності. $$OA=OB=R$$.
З другої властивості маємо $$\angle ACO=\angle BCO=\frac{\angle ACB}{2}=30^{\circ}$$.
З першого властивості випливає, що трикутники $$\triangle OAC$$ та $$\triangle OBC$$ прямокутні $$\left ( \angle OAC=\angle OBC=90^{\circ} \right ).$$ $$OA,AC$$ та $$OB,BC$$ – катети, $$OC$$ – гіпотенуза.
Відомо, що катет прямокутного трикутника, що лежить проти кута в 30°, дорівнює половині гіпотенузи, отже $$OC=2R$$.
Площа сфери обчислюється за формулою $$S=4\pi R^2$$, тоді радіус дорівнює $$R=\sqrt{\frac{S}{4\pi}}$$.
Тоді $$OC=2\sqrt{\frac{S}{4\pi}}$$.
Установимо відповідність між площею сфери (1-4) і відстанню від центру сфери до лінії перетину площин (А-Д).
$$OC=2\sqrt{\frac{36\pi}{4\pi}}=6$$ (см), тобто 1-Б.
$$OC=2\sqrt{\frac{12\pi}{4\pi}}=2\sqrt{3}$$ (см), тобто 2-В.
$$OC=2\sqrt{\frac{48\pi}{4\pi}}=4\sqrt{3}$$ (см), тобто 3-Д.
$$OC=2\sqrt{\frac{192\pi}{4\pi}}=8\sqrt{3}$$ (см), тобто 4-А.