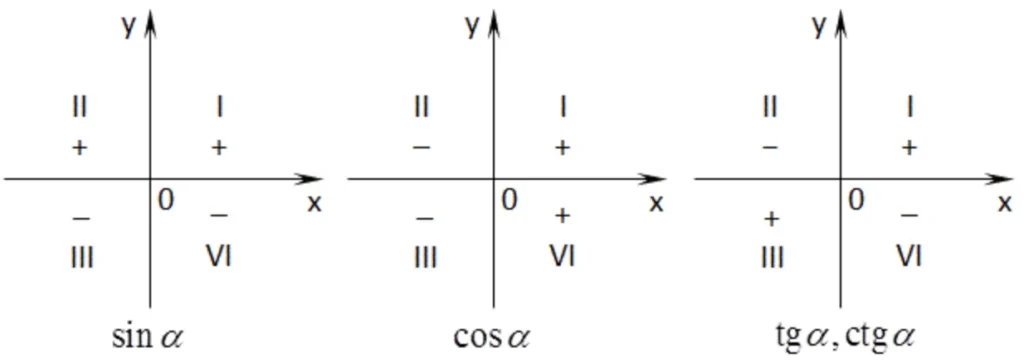
Для гострих кутів у декартовій системі координат
Нехай дана декартова система координат. З початку координат провели відрізок $$OM$$ під кутом $$\alpha$$ до осі $$Ox:$$
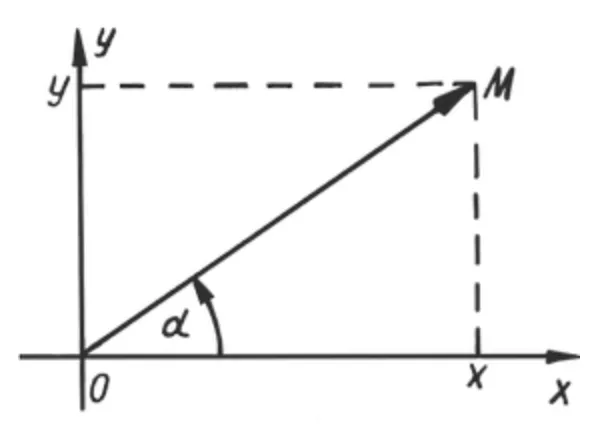
Синусом називається відношення:
$$\sin\alpha=\frac{y}{|OM|}$$
Косинусом називається відношення:
$$\cos\alpha=\frac{x}{|OM|}$$
Тангенсом називається відношення:
$$\text{tg}\alpha=\frac{y}{x}\;\left ( \alpha\neq\frac{\pi}{2}+k\pi,\; k\in\mathbb{Z} \right )$$
Котангенсом називається відношення:
$$\text{ctg}\alpha=\frac{x}{y}\;\left ( \alpha\neq k\pi,\; k\in\mathbb{Z} \right )$$
За допомогою одиничного кола
Розглянемо одиничне коло:
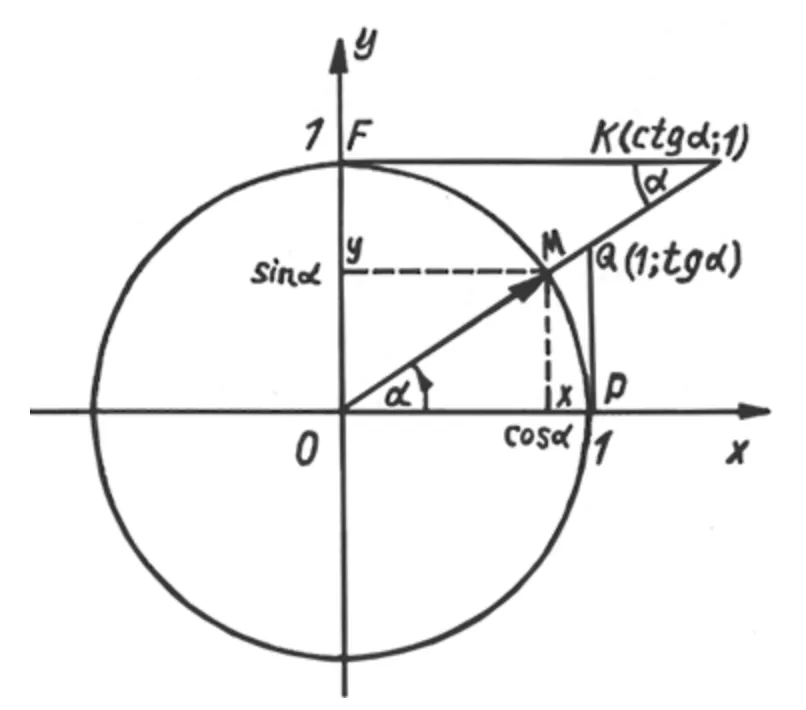
$$\sin\alpha=y$$
$$\cos\alpha=x$$
$$\text{tg}\alpha$$ – ордината точки $$Q$$
$$\text{ctg}\alpha$$ – абсциса точки $$K$$