Кілька основних способів вирішення рівнянь з модулем
Розглянемо основні способи розв’язування рівнянь з модулем на прикладах.
За визначенням модуля
$$|2-x|=2x-10$$
Визначення модуля: $$|a|=\left[\begin{matrix} a,& a\geqslant 0\\ -a,& a < 0 \end{matrix}\right.$$
$$\left[\begin{matrix} 2-x=2x-10 ,& 2-x\geqslant 0\\ x-2=2x-10, & 2-x < 0 \end{matrix}\right.$$
$$\left[\begin{matrix} x=4 ,& x\leqslant 2\\ x=8, & x>2 \end{matrix}\right.$$
Очевидно, що $$x=4$$ – сторонній корінь, бо $$4>2$$ і не задовольняє $$x\leqslant 2.$$
Таким чином, рішенням вихідного рівняння буде $$x=8$$
Відповідь: 8.
Зведення у квадрат
$$|2-x|=2x-10$$
Зведемо до квадрата обидві частини рівняння
$$|2-x|^2=(2x-10)^2$$
$$(2-x)^2=(2x-10)^2$$
$$4+x^2-4x=4x^2+100-40x$$
$$3x^2-36x+96=0$$
$$x^2-12x+32=0$$
Отримали квадратне рівняння, яке можна вирішити будь-яким з відомих нам способів.
$$x_1=4, x_2=8$$
Через те, що при зведенні у квадрат ми могли отримати сторонні корені, то необхідно виконати перевірку знайдених коренів, їх підставленням в початкове рівняння.
Перевіркою переконуємося, що $$x=4$$ – сторонній корінь.
Відповідь: 8.
Метод інтервалів
Даний метод полягає в наступному:
1) визначаються нулі кожного з модулів, що входить в рівняння (прирівнюємо нулю вирази під модулем)
2) На числовій прямій відзначаються знайдені значення, розбиваючи при цьому пряму на проміжки
3) Вирішують рівняння на кожному з проміжків
$$|2-x|=2x-10$$
$$2-x=0$$
$$x=2$$
Число 2 розбиває числову пряму на два проміжки $$(-\infty;2]\cup(2;+\infty)$$
I. Розглянемо рішення при $$x\in(-\infty;2]$$
$$|2-x|=2-x$$
$$2-x=2x-10$$
$$x=4\notin(-\infty;2]$$ – сторонній корінь
II. Розглянемо рішення при $$x\in(2;+\infty)$$
$$|2-x|=x-2$$
$$x-2=2x-10$$
$$x=8\in(2;+\infty)$$ – корінь рівняння
Відповідь: 8.
При розв’язанні рівнянь рекомендуємо враховувати властивості функцій і виділяти додаткові умови
$$|2-x|=2x-10$$
Через те, що модуль є невід’ємною величиною, то і права частина рівняння має бути невід’ємною, тобто $$2x-10\geqslant 0.$$
Значить додатковою умовою буде $$x\geqslant 5.$$
При таких значеннях $$x$$ вираз під модулем приймає від’ємне значення і модуль розкриється з протилежним знаком.
$$x-2=2x-10$$
$$x=8>5$$ (задовольняє додатковій умові) – корінь
Відповідь: 8.
Графічний спосіб розв’язування
Графічний спосіб полягає в наступному:
1) Ліва і права частини рівняння – дві функції від змінної $$x.$$
2) Будуються графіки кожної з функцій
3) Точки перетину графіків функцій є шуканим рішенням
$$|2-x|=2x-10$$
$$y=|2-x|=\left[\begin{matrix} 2-x ,& x\leqslant 2\\ x-2, & x>2 \end{matrix}\right.,$$ $$y=2x-10$$
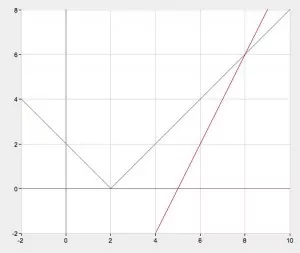
Точкою перетину графіків даних функцій буде точка $$(8;6),$$ тобто $$x=8$$
Відповідь: 8.
Графічний спосіб доречний, коли необхідно визначити кількість коренів, не знаходячи їх точних значень. Також даний метод досить часто застосовується при рішенні параметричних рівнянь.