Онлайн тест. ЗНО 2013 з математики (I сесія)

Обчисліть $$\frac{2^6\cdot5^6}{10^4}.$$

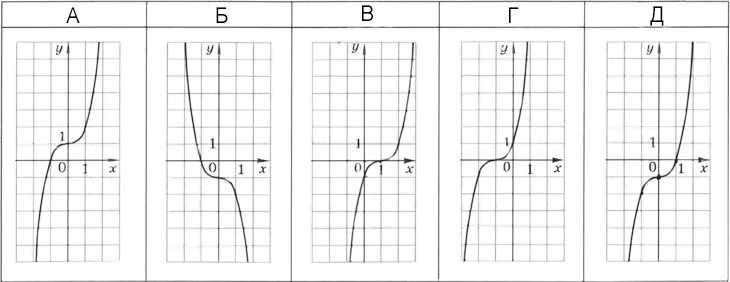
Укажіть ескіз графіка функції $$y=x^3-1.$$

Укажіть вираз, тотожно рівний виразу $$(2x+5)\cdot(3-x).$$

Пряма $$b$$ не має спільних точок з площиною $$\alpha.$$ Які з наведених тверджень є правильними?

І. Через пряму $$b$$ можна провести лише одну площину, перпендикулярну до площини $$\alpha.$$

ІІ. Через пряму $$b$$ можна провести лише одну площину, паралельну площині $$\alpha.$$

ІІІ. У площині $$\alpha$$ можна провести лише одну пряму, паралельну прямій $$b.$$

Визначте $$m$$ із співвідношення $$\frac{m}{2}=\frac{3}{n},$$ де $$n\neq0.$$

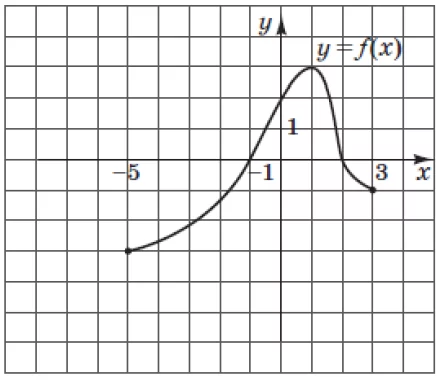
На рисунку зображено графік функції $$y=f(x),$$ визначеної на проміжку $$[-5;3].$$ Укажіть проміжок, на якому функція $$y=f(x)$$ зростає.

Розв’яжіть систему рівнянь $$\left\{\begin{matrix}2x &+&5y&=&5\\x&-&2y&=&7\end{matrix}\right..$$ Для одержаного розв’язку $$(x_0;y_0)$$ системи знайдіть суму $$x_0+y_0.$$

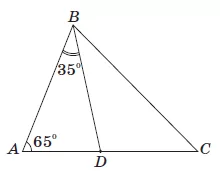
У трикутнику $$ABC: \angle A=65^{\circ}, BD$$ – бісектриса кута $$B$$ (див. рисунок). Знайдіть градусну міру кута $$BCA,$$ якщо $$\angle ABD=35^{\circ}.$$

Укажіть проміжок, якому належить рівняння $$\sqrt{1-x}=4.$$

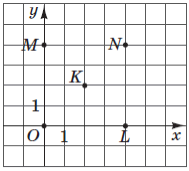
У координатній площині $$xy$$ зображено п’ять точок: $$O, L, N, M, K$$ (див. рисунок). Коло з центром в одній з цих точок дотикається до осі ординат у точці $$M.$$ У якій точці знаходиться центр цього кола?

В аріфметичній прогресії $$(a_n)$$ задано $$a_1=4, a_2=-1.$$ Укажіть формулу для знаходження n-го члена цієї прогресії.

Укажіть парну функцію.

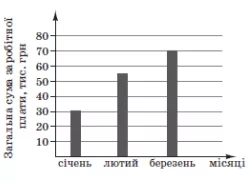
На діаграмі відображено нараховану фірмою загальну суму заробітної плати усім своїм працівникам у січні, лютому та березні 2011 року. У січні на фірмі працювали 15 співробітників, у лютому – 18, а в березні – 25. Як змінилася середня нарахована заробітна плата в цій фірмі в березні порівняно з січнем?

Розв’яжіть нерівність $$2^x\leqslant3.$$

Знайдіть площу повної поверхні куба, діагональ якого дорівнює $$2\sqrt{3}$$ см.

$$\log_{5}49+2\log_{5}\frac{5}{7}=$$

Менша сторона прямокутника дорівнює 16 м і утворює з його діагоналлю кут $$60^{\circ}.$$ Середини всіх сторін прямокутника послідовно сполучено. Знайдіть площу утвореного чотирикутника.

Укажіть нерівність, що виконується для $$\alpha\in(\frac{\pi}{2};\pi).$$

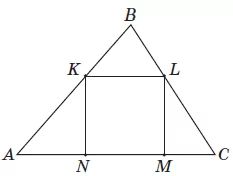
У трикутнику $$ABC$$ вписано квадрат $$KLMN$$ (див. рисунок). Висота цього трикутника, проведена до сторони $$AC,$$ дорівнює 6 см. Знайдіть периметр квадрата, якщо $$AC=10$$ см.

Переріз кулі площиною має площу $$81\pi$$ см². Знайдіть відстань від центра кулі до площини перерізу, якщо радіус кулі дорівнює 15 см.

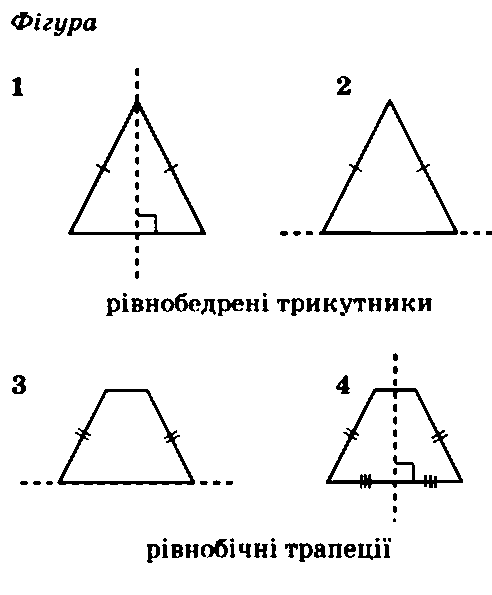
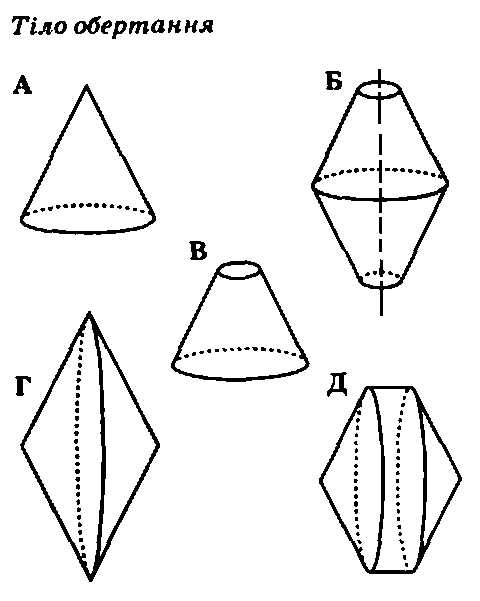
Установіть відповідність між фігурою (1-4) і тілом обертання (А-Д), яке утворено внаслідок обертання цієї фігури навколо прямої, зображеної пунктиром.

У прямокутній системі координат на площині $$xy$$ задано точки $$O(0;0)$$ і $$A(6;8).$$ З точки $$A$$ на вісь $$x$$ опущено перпендикуляр. Точка $$B$$ – основа цього перпендикуляра. Установіть відповідність між величиною та її числовим значенням.

Дві однакові автоматичні лінії виготовляють 16 т шоколадної глазурі за 4 дні. Установіть відповідність між запитаннями та правильною відповіддю на нього. Уважайте, що кожна лінія виготовляє однакову кількість глазурі щодня.

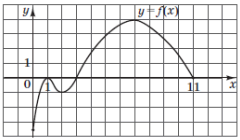
На рисунку зображено графік функції $$y=f(x),$$ визначеної на проміжку $$[0;11]$$ та диференційованої на проміжку $$(0;11).$$ Установіть відповідність між числом та проміжком, якому належить це число.

Додатне число $$A$$ більше додатного числа $$B$$ у 3.9 раза. На скільки відсотків число $$A$$ більше за число $$B?$$

Обчисліть значення виразу $$\frac{a^2-b^2}{a-b}-\frac{a^3-b^3}{a^2-b^2},$$ якщо $$a=-10.2; b=0.2.$$

Розв’яжіть нерівність $$\frac{4}{x+3}+\frac{6}{x}\geqslant1.$$

У відповіді запишіть суму всіх цілих її розв’язків.

Знайдіть найменший додатний період функції $$f(x)=9-6\cos(10\pi x+7).$$

В автобусному парку налічується $$n$$ автобусів, шосту частину яких було обладнано інформаційними табло. Пізніше інформаційні табло встановили ще на 5 автобусів з наявних у парку. Після проведеного переобладнання навмання вибирають один з $$n$$ автобусів парку. Ймовірність того, що це буде автобус з інформаційним табло, становить 0.25. Визначте $$n.$$ Уважайте, що кожен автобус обладнується лише одним табло.

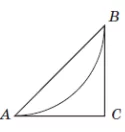
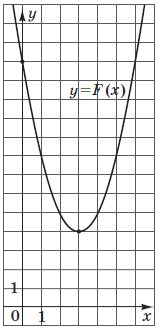
План паркової зони, обмеженої трикутником $$ABC,$$ зображено на рисунку. Дуга $$AB$$ – велосипедна доріжка. Відомо, що дуга $$AB$$ є четвертою частиною кола радіуса 1.6 км. $$CA$$ і $$CB$$ – дотичні до цього кола ($$A$$ і $$B$$ – точки дотику). Обчисліть площу зображеної на плані паркової зони (у км²).

На рисунку зображено графік функції $$F(x)=x^2+bx+c,$$ яка є первісною для функції $$f(x).$$ Визначте параметри $$b$$ і $$c,$$ знайдіть функцію $$f(x).$$ У відповіді запишіть значення $$f(-5).$$

Основою піраміди $$SABCD$$ є трапеція $$ABCD$$ $$(AD\parallel BC),$$ довжина середньої лінії якої дорівнює 5 см. Бічне ребро $$SB$$ перпендикулярне до площини основи піраміди і вдвічі більше від середньої лінії трапеції $$ABCD.$$ Знайдіть відстань від середини ребра $$SD$$ до площини $$SBC$$ (у см), якщо об’єм піраміди дорівнює 240 см³.

Знайдіть значення параметра $$a,$$ при якому корінь рівняння $$\lg(\sin 5\pi x)=\sqrt{16+a-x}$$ належить проміжку $$(1;\frac{3}{2}).$$