11 клас
Онлайн тест складено на основі деяких завдань пробного тестування зовнішнього незалежного оцінювання 2013 року з математики.
Тест триває 1 годину. Не поспішайте. Для переходу до потрібного завдання Ви можете скористатися блоком навігації вгорі тесту. Після проходження тесту Ви зможете ознайомитися з отриманими результатами та правильним розв’язанням завдань.
Тест
Підсумок тесту
Завершено завдань: 0 з 12
Завдання:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
Інформація
Бажаємо успіху!
Ви вже проходили тест раніше. Ви не можете пройти його знову.
Тест завантажується...
Щоб розпочати тест, потрібно ввійти або зареєструватися.
Щоб розпочати тест, потрібно завершити наступний тест:
Результати
Правильних відповідей: 0 з 12
Ваш час:
Час вийшов
Ви набрали 0 з 0 балів, (0)
Категорії
- Не присвоєно категорію 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- З відповіддю
- Позначене
- Завдання 1 з 12
1. Завдання
Кількість балів: 1Розташуйте в порядку зростання числа $$\frac{1}{9};\,0.1;\,0.11.$$
Правильно
Неправильно
Для того, щоб розташувати числа в порядку зростання, необхідно порівняти їх. Переведемо дроби у звичайні.
Згадаймо властивості:
- За однакових чисельників більший той дріб, у якого знаменник менший.
- За однакових знаменників більшим є той дріб, у якого чисельник більший.
$$\frac{1}{9}>\frac{1}{10}=0.1$$
$$0.11=\frac{11}{100}>\frac{10}{100}=\frac{1}{10}=0.1$$ (хоча для десяткових дробів одразу видно, що число $$0.11$$ розташоване на числовій осі правіше числа $$0.1$$)
$$0.11=\frac{11}{100}=\frac{99}{900}<\frac{100}{900}=\frac{1}{9}$$
Значить $$0.1<0.11<\frac{1}{9}$$
$$0.1;\,0.11;\,\frac{1}{9}$$ – розташовані в порядку зростання.
- Завдання 2 з 12
2. Завдання
Кількість балів: 1На рисунку зображено графік функції $$y=f(x)$$, яка визначена на відрізку $$[-4;3].$$ Укажіть область значень цієї функції.
 Правильно
Правильно
Неправильно
Область значень функції $$y=f(x)$$ — множина значень, яких набуває змінна $$y$$ у результаті застосування функції. Із графіка видно, що $$y\in[-1; 2].$$
- Завдання 3 з 12
3. Завдання
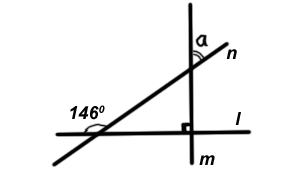
Кількість балів: 1Пряма $$n$$ перетинає перпендикулярні прямі $$l$$ і $$m$$ (див. рисунок). Визначте градусну міру кута $$a$$.
 Правильно
Правильно
Неправильно
Скористаємося властивостями суміжних і вертикальних кутів, сумою кутів прямокутного трикутника
$$a=90^{\circ}-(180^{\circ}-146^{\circ})=56^{\circ}$$
- Завдання 4 з 12
4. Завдання
Кількість балів: 1Діагоналі паралелограма $$ABCD$$ перетинаються в точці $$O$$ (див. рисунок). Укажіть правильну векторну рівність.
 Правильно
Правильно
Неправильно
$$\vec{CO}=\frac{1}{2}\vec{CA}=-\frac{1}{2}\vec{AC}=-\frac{1}{2}\left (\vec{AB}+\vec{AD} \right )$$
- Завдання 5 з 12
5. Завдання
Кількість балів: 1Розв’язати нерівність $$2x\geqslant x^2.$$
Правильно
Неправильно
$$x^2-2x\leqslant 0$$
$$x(x-2)\leqslant 0$$
Розв’язуємо методом інтервалів

$$x\in [0;2]$$
- Завдання 6 з 12
6. Завдання
Кількість балів: 1Обчислити $$\sqrt{2}\cdot\sqrt{0.08}.$$
Правильно
Неправильно
Використовуємо властивості коренів
$$\sqrt{2}\cdot\sqrt{0.08}=\sqrt{2\cdot0.08}=\sqrt{0.16}=\sqrt{(0.4)^2}=0.4$$
- Завдання 7 з 12
7. Завдання
Кількість балів: 1Спростіть вираз $$\frac{9-x^2}{x^2+6x+9}.$$
Правильно
Неправильно
Виконаємо перетворення, застосувавши формули скороченого множення
$$\frac{9-x^2}{x^2+6x+9}=\frac{(3-x)(3+x)}{(x+3)^2}=\frac{3-x}{x+3}$$
- Завдання 8 з 12
8. Завдання
Кількість балів: 1Діаметр основи конуса дорівнює 6 см, а площа його бічної поверхні – $$24\pi$$ см2. Знайдіть довжину твірної конуса.
Правильно
Неправильно
Діаметр основи конуса дорівнює 6 см, отже радіус дорівнює 3 см.
Площа бічної поверхні конуса знаходиться за формулою
$$S=\pi\cdot R\cdot l$$, де $$R$$ – радіус основи конуса, $$l$$ – твірна конуса. Оскільки площа бічної поверхні конуса дорівнює $$24\pi$$ см2, то твірна дорівнює
$$l=\frac{S}{R\pi}=\frac{24\pi}{3\pi}=8$$ см.
- Завдання 9 з 12
9. Завдання
Кількість балів: 4У лабораторії є два сплави міді з оловом: перший, масою 50 кг, містить 10% міді; другий, масою 100 кг, – містить 25% міді. Для кожного запитання підберіть правильну відповідь.
Елементи сортування
- 5
- 30
- 20
- 25
- 15
- Скільки кілограмів міді міститься в першому сплаві?
- Скільки кілограмів міді міститься у двох сплавах разом?
- Якщо з цих сплавів скласти новий сплав, то скільки відсотків міді міститиме цей сплав?
- Скільки кілограмів другого сплаву необхідно додати до першого, щоб створити сплав, який містить 15% міді?
Правильно
Неправильно
1) Скільки кілограмів міді міститься в першому сплаві?
Оскільки маса першого сплаву дорівнює 50 кг і в ньому міститься 10% міді, то
$$x_1$$ кг міді – 10%
50 кг першого сплаву – 100%
Отримали пропорцію
$$\frac{x_1}{50}=\frac{10\%}{100\%}\Rightarrow x_1=50\cdot 0.1=5$$ кг.
2) Скільки кілограмів міді міститься у двох сплавах одночасно?
Спочатку знайдемо масу міді в другому сплаві, а потім масу міді у двох сплавах одночасно.
$$x_2$$ кг міді – 25%
100 кг другого сплаву – 100%
$$\frac{x_2}{100}=\frac{25\%}{100\%}\Rightarrow x_2=100\cdot 0.25=25$$ кг
Оскільки маса міді в першому сплаві дорівнює 5 кг (див. 1), то
$$5+25=30$$ кг – загальна маса міді у двох сплавах одночасно
3) Якщо з цих сплавів утворити новий сплав, то скільки відсотків міді міститиме новий сплав?
Загальна маса міді у двох сплавах дорівнює 30 кг (див. 2)
Загальна маса двох сплавів дорівнює 50 + 100 = 150 кг – маса нового сплаву.
30 кг міді – p%
150 кг нового сплаву – 100%
$$\frac{30}{150}=\frac{p\%}{100\%}\Rightarrow p=\frac{1}{5}\cdot 100=20$$
4) Скільки кілограмів другого сплаву необхідно додати до першого, щоб вийшов сплав, що містить 15% міді?
Нехай необхідно додати $$y$$ кг другого сплаву з масою міді в ньому $$0.25y$$ кг (за умовою в другому сплаві 25% міді).
$$5+0.25y$$ кг міді – 15%
$$50+y$$ кг сплаву – 100%
$$\frac{5+0.25y}{50+y}=\frac{15\%}{100\%}$$
$$5+0.25y=0.15\cdot(50+y)$$
$$0.25y-0.15y=7.5-5$$
$$0.1y=2.5$$
$$y=25$$ кг
- Завдання 10 з 12
10. Завдання
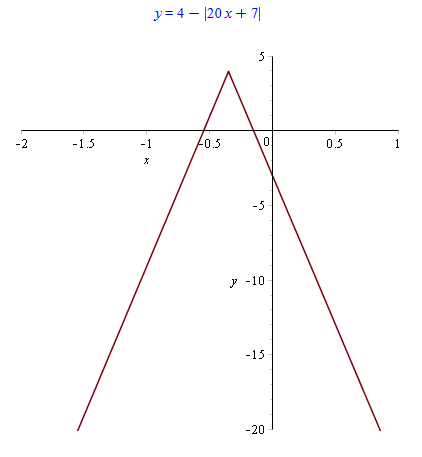
Кількість балів: 2За якого значення $$x$$ функція $$y=4-|20x+7|$$ досягає найбільшого значення?
Правильно
Неправильно
Скористаємося визначенням модуля і перетворимо функцію
$$y=4-|20x+7|=\left[\begin{matrix} 4-(20x+7), 20x+7\geqslant 0\\ \\ 4-(-20x-7), 20x+7< 0 \end{matrix}\right.=\left[\begin{matrix} -20x-3, x\geqslant -\frac{7}{20}\\ \\ 20x+11, x< -\frac{7}{20} \end{matrix}\right.$$
$$y=20x+11$$ зростаюча функція, а $$y=-20x-3$$ – спадаюча.
Отже, функція $$y=4-|20x+7|$$ зростає при $$x\in(-\infty;-\frac{7}{20})$$ і спадає при $$x\in[-\frac{7}{20};\infty)$$, а при $$x=-\frac{7}{20}=-0.35$$ набуває найбільшого значення (див. рисунок).
Графік функції $$y=4-|20x+7|$$

Відповідь: $$-0.35$$.
- Завдання 11 з 12
11. Завдання
Кількість балів: 2Обчислити $$\log_{b}a,$$ якщо $$\log_{3}a=8,\,\log_{3}b=5.$$
Правильно
Неправильно
Скористаємося формулою переходу до нової основи й отримаємо
$$\log_{b}a=\frac{\log_{3}a}{\log_{3}b}=\frac{8}{5}=1.6$$
Відповідь: 1.6.
- Завдання 12 з 12
12. Завдання
Кількість балів: 2Знайдіть найменше ціле значення параметра $$a$$, за якого рівняння $$\sqrt{x^2-5x}+\sqrt{x^2-9x+20}=\sqrt{a}\cdot\sqrt{x-5}$$ має два корені.
Правильно
Неправильно
Перетворимо ліву частину. У першому підкореневому виразі винесемо спільний множник за дужки. Для другого використаємо формулу розкладання квадратного тричлена на множники, знайшовши його корені за теоремою Вієта.
$$\sqrt{x(x-5)}+\sqrt{(x-4)(x-5)}=\sqrt{a}\cdot\sqrt{x-5}$$
ОДЗ:
$$\left\{\begin{matrix} x(x-5) & \geqslant & 0\\ (x-4)(x-5) & \geqslant & 0\\ x-5& \geqslant& 0\\ a& \geqslant & 0 \end{matrix}\right.\Rightarrow x\geqslant5,\;a\geqslant0$$
Застосуємо властивість коренів (корінь добутку)
$$\sqrt{x}\cdot\sqrt{x-5}+\sqrt{x-4}\cdot\sqrt{x-5}=\sqrt{a}\cdot\sqrt{x-5}$$
Винесемо спільний множник за дужки
$$\sqrt{x-5}\cdot(\sqrt{x}+\sqrt{x-4}-\sqrt{a})=0$$
Добуток дорівнює нулю, коли хоча б один із співмножників дорівнює нулю, отже
$$\sqrt{x-5}=0$$ или $$\sqrt{x}+\sqrt{x-4}-\sqrt{a}=0$$
$$x=5$$ или $$\sqrt{x}+\sqrt{x-4}=\sqrt{a}$$
$$x=5$$ є коренем рівняння і не залежить від параметра $$a$$
Розглянемо рівняння $$\sqrt{x}+\sqrt{x-4}=\sqrt{a}$$
Ліва і права частина рівняння невід’ємні ($$\sqrt{}$$ $$\geqslant 0$$). Зведемо у квадрат обидві частини рівняння
$$\left (\sqrt{x}+\sqrt{x-4} \right )^2=\left (\sqrt{a} \right )^2$$
Розкриємо дужки, використовуючи властивості коренів і формулу квадрата суми
$$x+x-4+2\sqrt{x(x-4)}=a$$
$$2\sqrt{x(x-4)}=a+4-2x$$
Ліва частина невід’ємна, отже, і права частина має бути невід’ємною. Отримали додаткову умову $$a+4-2x\geqslant 0\Rightarrow x\leqslant \frac{a+4}{2}$$
З урахуванням ОДЗ
$$5\leqslant x\leqslant \frac{a+4}{2}\Rightarrow \frac{a+4}{2}\geq 5\Rightarrow a\geq 6$$
Зведемо у квадрат обидві частини рівняння
$$\left (2\sqrt{x(x-4)} \right )^2=\left (a+4-2x \right )^2$$
$$4x(x-4)=(a+4)^2+4x^2-4x(a+4)$$
$$4x^2-16x=(a+4)^2+4x^2-16x-4ax$$
$$4ax=(a+4)^2$$
$$x=\frac{(a+4)^2}{4a}$$
Знайдемо найменше ціле значення параметра, за якого знайдений $$x$$ є коренем рівняння
$$\frac{(a+4)^2}{4a}\geqslant 5$$
$$\frac{(a+4)^2}{4a}-5\geqslant 0$$
$$\frac{(a+4)^2-20a}{4a}\geqslant 0$$
$$\frac{a^2+16+8a-20a}{4a}\geqslant 0$$
$$\frac{a^2-12a+16}{4a}\geqslant 0$$
$$a\geqslant 6\Rightarrow 4a>0\Rightarrow a^2-12a+16\geqslant 0$$
Розглянемо $$a^2-12a+16=0$$
Знайдемо корені (скористаємося формулою дискримінанта для парного коефіцієнта при першому ступені)
$$D_1=36-16=20=2^2\cdot5$$
$$a_{1,2}=6\pm2\sqrt{5}$$
$$\left [a-(6-2\sqrt{5}) \right ]\cdot\left [a-(6+2\sqrt{5}) \right ]\geqslant 0$$
$$a\geqslant 6\Rightarrow a-(6-2\sqrt{5}) >0\Rightarrow a-(6+2\sqrt{5})\geqslant 0\Rightarrow a\geqslant 6+2\sqrt{5}$$
$$6+2\sqrt{5} \approx 10.47$$
Отже, найменше ціле значення параметра $$a=11$$, за якого вихідне рівняння має два корені
$$x_1=5,\;x_2=\frac{(11+4)^2}{4\cdot11}=\frac{225}{44}=5\frac{5}{44}$$
Відповідь: $$a=11.$$