Задача
Село розташоване на березі річки, а школа – на шосе, що перетинає річку під прямим кутом.
Взимку школяр ходить із села до школи навпростець на лижах і витрачає на дорогу 40 хв. Навесні, у розпусницю, він іде берегом річки до шосе, а далі – шосе до школи, і витрачає на дорогу 1 год 10 хв. Нарешті, восени він проходить уздовж річки половину відстані, що відокремлює село від шосе, а далі йде навпростець. При цьому він доходить до школи швидше, ніж за 57 хв.
Установіть, що далі: село від шосе чи школа від річки, якщо відомо, що пішки школяр ходить завжди з однією і тією самою швидкістю, а на лижах зі швидкістю на 25% більшою (річку і шосе вважати прямими лініями).
Рішення
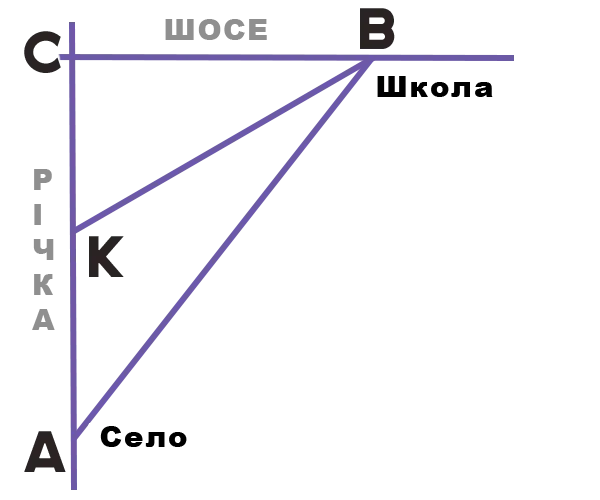
Введемо позначення.
$$A$$ – місце розташування села, $$B$$ – місце розташування школи, $$C$$ – точка перетину річки та шосе.
$$\triangle ABC$$: $$\angle C=90^{\circ}$$, $$AB=c$$, $$AC=b$$, $$BC=a$$. Точка $$K$$ – середина відстані від села до шосе вздовж річки, $$AK=KC=\frac{b}{2}$$, $$BK=\sqrt{a^2+(\frac{b}{2})^2}$$ – відстань від половини шляху річкою до школи (за теоремою Піфагора з прямокутного трикутника $$\triangle KCB$$).
Візьмемо за одиницю швидкість пішого пересування школяра, тоді швидкість на лижах дорівнює $$1.25$$
Знайдемо час, за який може дістатися школяр із села до школи навпростець, якщо йтиме пішки: $$1.25\cdot 40=50$$ хвилин.
ЗИМА: відстань $$c$$ за 40 хвилин на лижах або 50 хвилин пішки.
ВЕСНА: відстань $$a+b$$ 70 хвилин пішки.
ОСІНЬ: відстань $$\frac{b}{2}+\sqrt{a^2+(\frac{b}{2})^2}$$ менш ніж за 57 хвилин пішки.
Отже, $$a+b=70$$, тоді $$b=70-a$$
З трикутника $$\triangle ABC$$ за теоремою Піфагора $$a^2+b^2=c^2$$
$$a^2+(70-a)^2=50^2$$
$$a^2+70^2+a^2-140a-50^2=0$$
$$2a^2-140a+(70-50)(70+50)=0$$
$$2a^2-140a+2400=0$$
$$a^2-70a+1200=0$$
За теоремою Вієта: $$a_1=30$$, $$a_2=40$$
Тоді $$b_1=40$$, $$b_2=30$$
Перевіримо осінню нерівність $$\frac{b}{2}+\sqrt{a^2+(\frac{b}{2})^2} < 57$$
- $$a=30$$, $$b=40$$
$$\frac{40}{2}+\sqrt{30^2+(\frac{40}{2})^2} < 57$$
$$\sqrt{900+400} < 37$$
$$\sqrt{1300} < \sqrt{1369}$$ – вірно - $$a=40$$, $$b=30$$
$$\frac{30}{2}+\sqrt{40^2+(\frac{30}{2})^2} < 57$$
$$\sqrt{1600+225} < 42$$
$$\sqrt{1825} < \sqrt{1764}$$ – помилково
Отже, відстань від села до шосе дорівнює 40, що більше відстані від школи до річки, яка дорівнює 30.
Відповідь: село далі від шосе, ніж школа від річки.