1 Варіант
Пропонуємо Вашій увазі розв’язання першого варіанта підсумкової контрольної роботи з алгебри за 7 клас.
Частина 1
Завдання 1
Обчислити значення виразу $$\frac{(2^2)^3\cdot2^5}{2^9}.$$
А. 2
Б. 4
В. 1
Г. 8
Рішення
Використовуємо властивості ступенів
$$\frac{(2^2)^3\cdot2^5}{2^9}=2^{2\cdot3+5-9}=2^2=4$$
Відповідь: Б.
Завдання 2
Якому одночлену дорівнює вираз $$3ab^4\cdot(-2a^2b^3)?$$
А. $$-6a^3b^7$$
Б. $$6a^3b^7$$
В. $$-6a^2b^12$$
Г. $$6a^2b^12$$
Рішення
Використовуємо визначення одночлена та властивості ступенів
$$3ab^4\cdot(-2a^2b^3)=-2\cdot3\cdot a^{1+2}\cdot b^{4+3}=-6a^3b^7$$
Відповідь: А.
Завдання 3
Перетворити в многочлен вираз $$(a-5b)^2.$$
А. $$a^2-25b^2$$
Б. $$a^2-5ab+5b^2$$
В. $$a^2+2ab+25b^2$$
Г. $$a^2-10ab+25b^2$$
Рішення
Використовуємо формули скороченого множення
$$(a-5b)^2=a^2+(5b)^2-2\cdot a\cdot (5b)=a^2-10ab+25b^2$$
Відповідь: Г.
Завдання 4
Через яку з даних точок проходить графік рівняння $$5x+4y=20?$$
А. $$A(-4;0)$$
Б. $$B(3;1)$$
В. $$C(0;5)$$
Г. $$D(2;3)$$
Рішення
Перевіряємо точки підставлянням в рівняння.
$$5\cdot(-4)+4\cdot0=-20\neq20$$
$$5\cdot(3)+4\cdot1=19\neq20$$
$$5\cdot(0)+4\cdot5=20$$
$$5\cdot(2)+4\cdot3=22\neq20$$
Оскільки рівність $$5\cdot(0)+4\cdot5=20$$ вірна, графік рівняння $$5x+4y=20$$ проходить через точку $$C(0;5).$$
Відповідь: В.
Частина 2
Завдання 5
Розкласти многочлен на множники $$9a-27a^4.$$
Рішення
Використовуємо основні способи розкладання многочленів на множники
$$9a-27a^4=9a(1-3a^3)$$
Відповідь: $$9a(1-3a^3).$$
Завдання 6
Знайти корінь рівняння $$(x-4)(x-6)-(x-2)(x+2)=-2.$$
Рішення
Розкриємо перші дужки й застосуємо до других дужок формулу різниці квадратів
$$x^2-6x-4x+24-(x^2-4)=-2$$
$$x^2-6x-4x+24-x^2+4=-2$$
$$-10x+28=-2$$
$$-10x=-2-28$$
$$-10x=-30$$
$$x=3$$
Відповідь: 3.
Завдання 7
Розв’язати систему рівнянь $$\left\{\begin{matrix} x & + & y & = & 5\\ 3x & + & 2y & = & 11 \end{matrix}\right..$$
Рішення
$$\left\{\begin{matrix} x & + & y & = & 5 & (1)\\ 3x & + & 2y & = & 11 & (2)\end{matrix}\right.$$
З другого рівняння системи віднімемо перше, помножене на три: $$(2)-3\cdot(1)$$
$$3x-3x+2y-3y=11-15$$
$$-y=-4$$
$$y=4$$
Підставимо значення $$y=4$$ у перше рівняння системи й знайдемо $$x$$
$$x+4=5$$
$$x=1$$
Відповідь: $$(1;4).$$
Частина 3
Завдання 8
Побудуйте графік функції $$y=4-2x.$$ Користуючись побудованим графіком, установіть, за яких значень аргументу функція набуває від’ємних значень.
Рішення
$$y=4-2x$$ – лінійна функція. Графіком лінійної функції є пряма лінія. Пряму можна провести через дві точки. Складемо таблицю значень даної функції для двох довільних значень аргументу:
| $$x$$ | 0 | 2 |
| $$y$$ | 4 | 0 |
Проведемо пряму через отримані точки $$(0;4)$$ та $$(2;0).$$
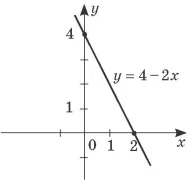
$$y=4-2x$$
Функція $$y=4-2x$$ набуває від’ємних значень, коли її графік лежить нижче за вісь абсцис, тобто при $$x > 2.$$
Відповідь: при $$x > 2.$$
Завдання 9
Маса 2 злитків олова і 5 злитків свинцю становить 33 кг, а маса 6 злитків олова і 2 злитків свинцю – 34 кг. Визначити масу одного злитка олова й одного злитка свинцю.
Рішення
Нехай маса одного злитка олова дорівнює $$x$$ кг, а маса одного злитка свинцю — $$y$$ кг. Маса двох злитків олова і п’яти злитків свинцю становить $$(2x+5y)$$ кг, що за умовою дорівнює 33 кг. Отримали перше рівняння системи $$2x+5y=33.$$
Аналогічно складемо друге рівняння системи $$6x+2y=34.$$
Необхідно розв’язати систему двох рівнянь із двома невідомими $$\left\{\begin{matrix} 2x & + & 5y & = & 33\\ 6x & + & 2y & = & 34 \end{matrix}\right..$$
Помножимо перше рівняння системи на 3 і віднімемо його від другого:
$$6x-6x+2y-15y=34-99$$
$$-13y=-65$$
$$y=5$$
Отже, маса одного злитка свинцю дорівнює 5 кг.
Підставимо знайдене значення $$y=5$$ у перше рівняння системи і знайдемо $$x$$
$$2x+25=33$$
$$2x=8$$
$$x=4$$
Отже, маса одного злитка олова дорівнює 4 кг.
Відповідь: 4 кг; 5 кг.
Завдання 10
Яке найменше значення і за якого значення змінної приймає вираз $$x^2-4x-5?$$
Рішення
Виділимо повний квадрат, скориставшись формулами скороченого множення
$$x^2-4x-5=x^2-2\cdot2\cdot x+2^2-2^2-5=(x^2-2\cdot2\cdot x+2^2-2^2)-4-5=(x-2)^2-9$$
Оскільки вираз $$(x-2)^2$$ за будь-яких значень $$x$$ невід’ємно, тобто $$(x-2)^2\geqslant0$$ при $$x\in\mathbb{R},$$ то
$$(x-2)^2-9\geqslant-9,$$ причому найменше значення $$-9$$ цей вираз приймає при $$x=2.$$
Відповідь: $$-9$$ при $$x=2.$$