Зовнішнє незалежне оцінювання 2012 з математики
Пройдіть онлайн тест першої сесії зовнішнього незалежного оцінювання з математики за 2012 рік, щоб дізнатися, наскільки ви підготовлені до складання тестів ЗНО. Цей безплатний онлайн тест складається з 32 тестових завдань.
Як нараховуються бали
Завдання 1-20 оцінюються по 1 балу (за правильну відповідь), завдання 21-24 – по 4 бали (по 1 балу за кожну правильну логічну пару) та за завдання 25-32 нараховується по 2 бали (за правильну числову відповідь).
Як відповідати на тестові завдання
Для тестових завдань 1-20 оберіть правильний, на Ваш погляд, варіант відповіді та натисніть кнопку Далі.
Для тестових завдань 21-24 на встановлення відповідності розташуйте (перетягніть мишкою) елементи сортування навпроти тверджень так, щоб утворилася правильна логічна пара і натисніть кнопку Далі.
Для тестових завдань 25-32 із числовими відповідями розглянемо на прикладах:
- Якщо у вас вийшло ціле позитивне число, наприклад 7, то в поле відповіді введіть 7 і натисніть кнопку Далі;
- Якщо у вас вийшло ціле від’ємне число, наприклад -326, то в поле відповіді введіть -326 і натисніть кнопку Далі;
- Якщо у вас вийшло дробове додатне число, наприклад 93.7, то в поле відповіді введіть 93.7 (використовуйте крапку) і натисніть кнопку Далі;
- Якщо у вас вийшло дробове від’ємне число, наприклад -12.61, то в поле відповіді введіть -12.61 (використовуйте точку) і натисніть кнопку Далі.
Тривалість тесту
Тест триває 2 години 30 хвилин. Не поспішайте. Якщо Ви пропустите запитання, то можете повернутися до нього пізніше, натиснувши на кнопку Назад, або скористатися навігацією завдань.
Увага!!!
Якщо ви на останньому завданні натиснете кнопку Далі, то тест буде завершено. Також тест буде завершено автоматично після закінчення відведеного часу.
Тест
Підсумок тесту
Завершено завдань: 0 з 32
Завдання:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
Інформація
Бажаємо успіху!
Ви вже проходили тест раніше. Ви не можете пройти його знову.
Тест завантажується...
Щоб розпочати тест, потрібно ввійти або зареєструватися.
Щоб розпочати тест, потрібно завершити наступний тест:
Результати
Правильних відповідей: 0 з 32
Ваш час:
Час вийшов
Ви набрали 0 з 0 балів, (0)
Категорії
- Не присвоєно категорію 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- З відповіддю
- Позначене
- Завдання 1 з 32
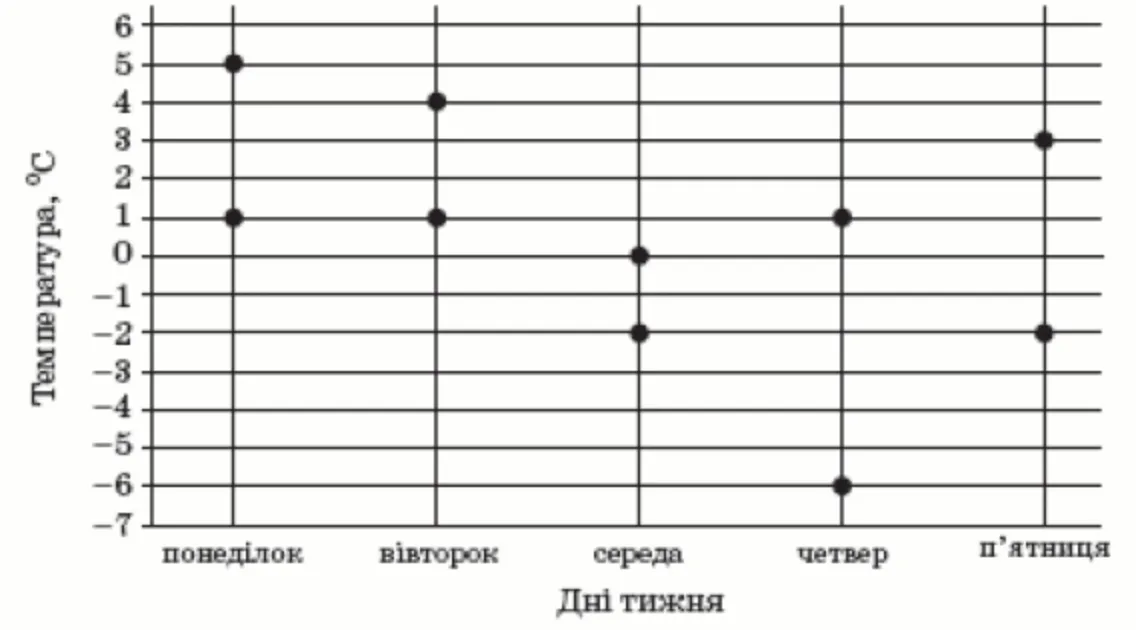
1. Завдання
Кількість балів: 1На рисунку показано жирними точками найвищу і найнижчу температури повітря кожного дня тижня з понеділка до п’ятниці в деякому місті України. По горизонталі відмічено дні тижня, а по вертикалі – температуру повітря в градусах Цельсія. У який день різниця між найвищою та найнижчою температурами повітря була найбільшою?
 Правильно
Правильно
Неправильно
- Завдання 2 з 32
2. Завдання
Кількість балів: 1Протягом тижня два кур’єри разом доставили 210 пакетів. Кількості пакетів, доставлених першим і другим кур’єрами за цей період, відносяться як 3:7. Скільки пакетів доставив другий кур’єр?
Правильно
Неправильно
- Завдання 3 з 32
3. Завдання
Кількість балів: 1Яка з наведених точок лежить у площині $$Oxz$$ прямокутної системи координат у просторі?
Правильно
Неправильно
- Завдання 4 з 32
4. Завдання
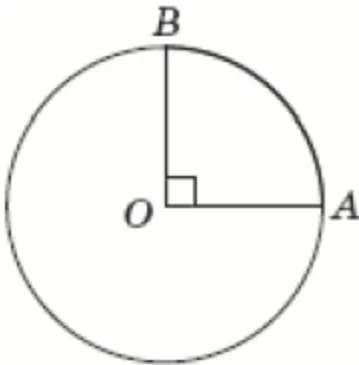
Кількість балів: 1На рисунку зображено коло з центром в точці $$O,$$ довжина якого дорівнює 64 см. Визначте довжину меншої дуги $$AB$$ кола, якщо $$\angle AOB=90^{\circ}.$$
 Правильно
Правильно
Неправильно
- Завдання 5 з 32
5. Завдання
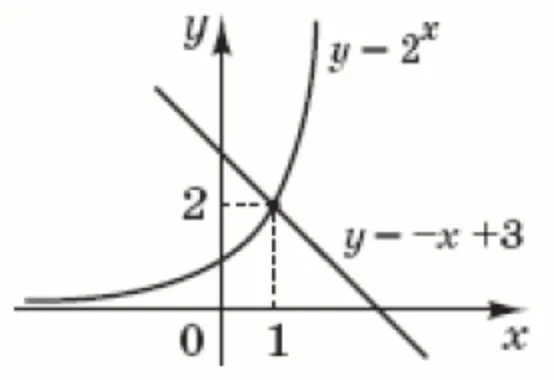
Кількість балів: 1Використовуючи зображені на рисунку графіки функцій, розв’яжіть нерівність $$2^x>-x+3.$$
 Правильно
Правильно
Неправильно
- Завдання 6 з 32
6. Завдання
Кількість балів: 1При якому значенні $$y$$ вектори $$\vec{a}(-3;5)$$ і $$\vec{b}(6;y)$$ колінеарні?
Правильно
Неправильно
- Завдання 7 з 32
7. Завдання
Кількість балів: 1Укажіть область визначення функції $$\log_{3}(x+9).$$
Правильно
Неправильно
- Завдання 8 з 32
8. Завдання
Кількість балів: 1Укажіть хибне твердження.
Правильно
Неправильно
- Завдання 9 з 32
9. Завдання
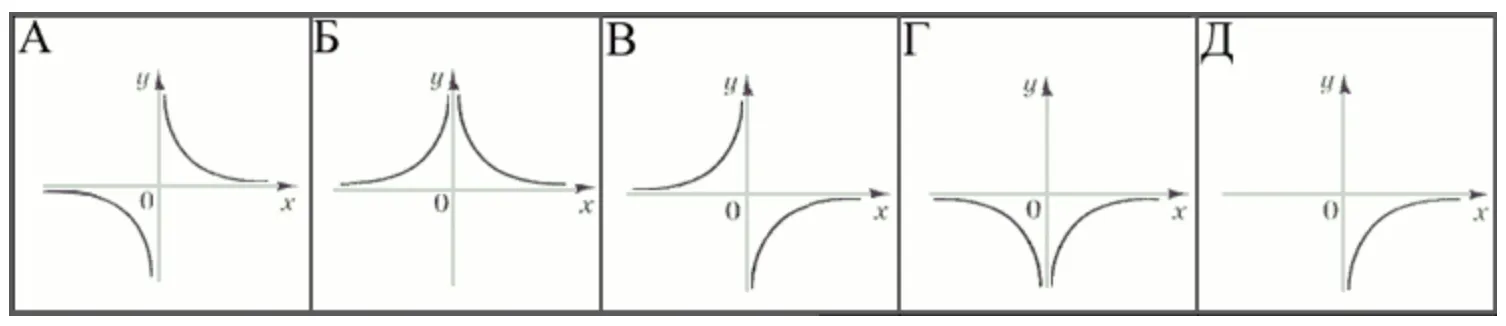
Кількість балів: 1На якому з наведених рисунків зображено ескіз графіка функції $$y=-\frac{1}{x}?$$
 Правильно
Правильно
Неправильно
- Завдання 10 з 32
10. Завдання
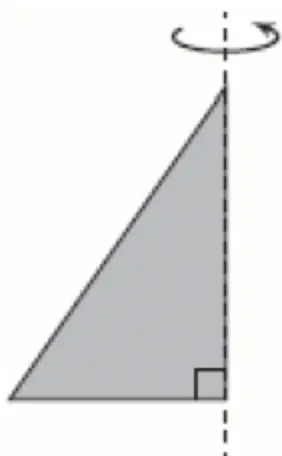
Кількість балів: 1Прямокутний трикутник із катетами 9 см і 12 см обертається навколо більшого катета (див. рисунок). Визначте площу повної поверхні отриманого тіла обертання.
 Правильно
Правильно
Неправильно
- Завдання 11 з 32
11. Завдання
Кількість балів: 1У магазині побутової техніки діє акція: на першу велику покупку (вартість перевищує 1000 грн) надається знижка 30 грн, на кожну наступну велику покупку попередня знижка збільшується на 25 грн. На яку за рахунком велику покупку отримає в цьому магазині покупець знижку 180 грн?
Правильно
Неправильно
- Завдання 12 з 32
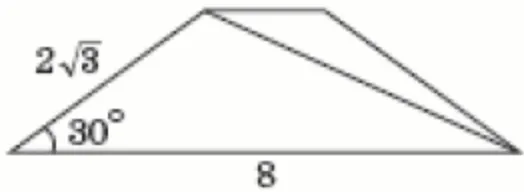
12. Завдання
Кількість балів: 1На рисунку зображено рівнобічну трапецію, бічна сторона якої дорівнює $$2\sqrt{3},$$ а більша основа – 8. Визначте довжину діагоналі цієї трапеції, якщо її гострий кут дорівнює $$30^{\circ}.$$
 Правильно
Правильно
Неправильно
- Завдання 13 з 32
13. Завдання
Кількість балів: 1Порожній басейн, що вміщує x м3 води, повністю заповнюють водою за 5 годин (швидкість заповнення є сталою). За якою формулою можна обчислити кількість води V (у м3) у басейні через 2 години після початку його заповнення, якщо басейн був порожній і швидкість заповнення не змінювалась?
Правильно
Неправильно
- Завдання 14 з 32
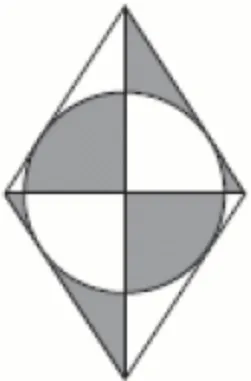
14. Завдання
Кількість балів: 1На рисунку зображено ромб, площа якого дорівнює 96 см2. У ромб вписано коло. Визначте площу зафарбованої фігури.
 Правильно
Правильно
Неправильно
- Завдання 15 з 32
15. Завдання
Кількість балів: 1Укажіть проміжок, якому належить значення виразу $$\text{ctg}\,25^{\circ}.$$
Правильно
Неправильно
- Завдання 16 з 32
16. Завдання
Кількість балів: 1Висота правильної чотирикутної піраміди дорівнює 3 см, а бічне ребро – 5 см. Визначте косинус кута між бічним ребром і площиною основи.
Правильно
Неправильно
- Завдання 17 з 32
17. Завдання
Кількість балів: 1Розв’яжіть нерівність $$(x+4)(x-7)>3(x-7).$$
Правильно
Неправильно
- Завдання 18 з 32
18. Завдання
Кількість балів: 1Запишіть числа $$2^{15},\;4^{10},\;10^5$$ у порядку зростання.
Правильно
Неправильно
- Завдання 19 з 32
19. Завдання
Кількість балів: 1Якщо $$a<-2,$$ то $$1-|a+2|=$$
Правильно
Неправильно
- Завдання 20 з 32
20. Завдання
Кількість балів: 1Функція $$f(x)$$ в точці $$x_0=5$$ має похідну $$f'(5)=-1.$$ Обчисліть значення похідної функції $$g(x)=f(x)\cdot x$$ в точці $$x_0,$$ якщо $$f(5)=3.$$
Правильно
Неправильно
- Завдання 21 з 32
21. Завдання
Кількість балів: 4До кожного виразу доберіть тотожно рівний йому вираз.
Елементи сортування
- $$a^2-64$$
- $$a^2-16a+64$$
- $$a^3-64$$
- $$a^2-20a+64$$
- $$a^3+64$$
- $$(a-8)(a+8)$$
- $$(a-8)^2$$
- $$(a-4)(a^2+4a+16)$$
- $$(a-4)(a-16)$$
Правильно
Неправильно
- Завдання 22 з 32
22. Завдання
Кількість балів: 4Розв’яжіть рівняння. Установіть відповідність між кожним рівнянням та твердженням, що є правильним для цього рівняння.
Елементи сортування
- корінь рівняння належить відрізку $$[-2;2]$$
- коренем рівняння є ірраціональне число
- рівняння не має коренів
- коренем рівняння є число 16
- рівняння має два корені
- $$\frac{x-1}{x+7}=0$$
- $$x+\pi=0$$
- $$\cos x=\sqrt{3}$$
- $$\sqrt{x}=4$$
Правильно
Неправильно
- Завдання 23 з 32
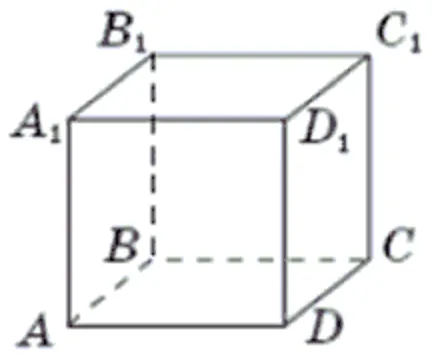
23. Завдання
Кількість балів: 4На рисунку зображено куб $$ABCDA_1B_1C_1D_1.$$ Установіть відповідність між парою прямих та їхніми взаємним розміщенням.

Елементи сортування
- прямі паралельні
- прямі перетинаються і утворюють кут $$60^{\circ}$$
- прямі мимобіжні
- прямі перетинаються і утворюють прямий кут
- прямі перетинаються і утворюють кут $$45^{\circ}$$
- $$AB_1,\; C_1D$$
- $$AC,\; CD_1$$
- $$AB_1,\; CD_1$$
- $$AC,\; CC_1$$
Правильно
Неправильно
- Завдання 24 з 32
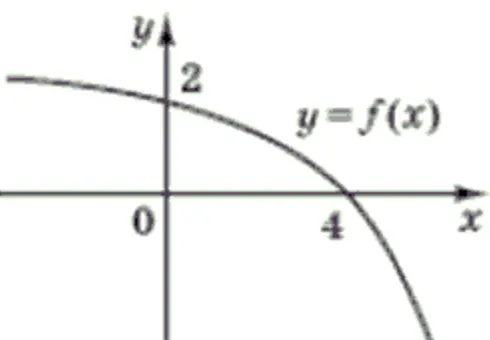
24. Завдання
Кількість балів: 4На рисунку зображено графік функції $$y=f(x),$$ спадної на проміжку $$(-\infty;\infty).$$ Установіть відповідність між функцією та точкою перетину її графіка з віссю $$Ox.$$

Елементи сортування
- $$(4;0)$$
- $$(0;0)$$
- $$(2;0)$$
- $$(6;0)$$
- $$(8;0)$$
- $$y=2f(x)$$
- $$y=f(x)-2$$
- $$y=f(x+2)$$
- $$y=f(x-2)$$
Правильно
Неправильно
- Завдання 25 з 32
25. Завдання
Кількість балів: 2Петро, Микола та Василь уранці відвідали кафе і кожен із них замовив собі на сніданок бутерброд та гарячий напій. Відомо, що Василь не п’є чорного чаю, а Микола замовив собі бутерброд із шинкою. Скориставшись таблицею, визначте, скільки грошей (у грн) буде коштувати Миколі, Василю і Петру разом найдешевше замовлення в цьому кафе.
Страви Ціна, грн Бутерброд із сиром 7.00 Бутерброт із шинкою 15.00 Бутерброд із рибою 17.00 Кава з молоком 13.00 Кава 12.00 Чай чорний 8.00 Чай зелений 9.00 Правильно
Неправильно
- Завдання 26 з 32
26. Завдання
Кількість балів: 2Скільки всього різних двоцифрових чисел можна утворити з цифр 1, 5, 7 і 8 так, щоб у кожному числі всі цифри не повторювалися?
Правильно
Неправильно
- Завдання 27 з 32
27. Завдання
Кількість балів: 2Розв’яжіть систему $$\left\{\begin{matrix} y & + & x & = &3 \\ x^2& + & 4 & = & 8y \end{matrix}\right..$$
Якщо пара $$(x_0;y_0)$$ є єдиним розв’язком цієї системи, то запишіть у відповідь добуток $$x_0\cdot y_0.$$ Якщо пари $$(x_1;y_1)$$ та $$(x_2;y_2)$$ є розв’язками цієї системи рівнянь, то запишіть у відповідь найменший із добутків $$x_1\cdot y_1$$ та $$x_2\cdot y_2.$$
Правильно
Неправильно
- Завдання 28 з 32
28. Завдання
Кількість балів: 2Бісектриса кута $$A$$ прямокутника $$ABCD$$ перетинає його більшу сторону $$BC$$ в точці $$M.$$ Визначте радіус кола (у см), описаного навколо прямокутника, якщо $$BC = 24$$ см, $$AM = 10\sqrt{2}$$ см.
Правильно
Неправильно
- Завдання 29 з 32
29. Завдання
Кількість балів: 2Обчисліть $$(\sqrt{20})^{2+\log_{20}16}.$$
Правильно
Неправильно
- Завдання 30 з 32
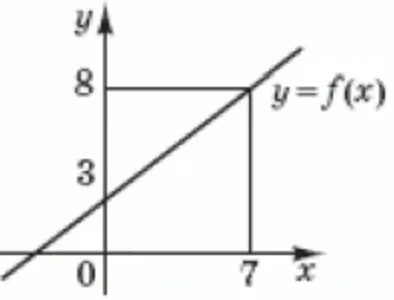
30. Завдання
Кількість балів: 2Обчисліть $$\int_{0}^{7}f(x)dx,$$ використовуючи зображений на рисунку графік лінійної функції $$y=f(x).$$
 Правильно
Правильно
Неправильно
- Завдання 31 з 32
31. Завдання
Кількість балів: 2За основою прямої трикутної призми $$ABCA_1B_1C_1$$ є рівнобедрений трикутник $$ABC,$$ де $$AB=BC=25$$ см, $$AC=30$$ см. Через бічне ребро $$AA_1$$ призми проведено площину, перпендикулярну до ребра $$BC.$$ Визначте об’єм призми (у см3), якщо площа утвореного перерізу дорівнює 72 см2.
Правильно
Неправильно
- Завдання 32 з 32
32. Завдання
Кількість балів: 2При якому найменшому значенні $$a$$ рівняння
$$\sqrt{x-2+2\sqrt{x-3}}+(14-2a)\cdot\sqrt[4]{x-3}+32=6a$$
має хоча б один корінь?
Правильно
Неправильно