Пропонуємо Вашій увазі розв’язання тестових завдань другої частини першого варіанта ДПА 2012 з математики для одинадцятого класу.
Друга частина атестаційної роботи складається з чотирьох завдань відкритої форми з короткою відповіддю.
Завдання 2.1
Розв’язати рівняння $$4^x+2^{x+1}=80.$$
Рішення
Скористаємося властивостями ступенів
$$(2^2)^x+2\cdot2^x-80=0$$
$$(2^x)^2+2\cdot2^x-80=0$$
Заміна $$2^x=t> 0$$
$$t^2+2t-80=0$$
За теоремою Вієта:
$$t_1=-10$$ (сторонній корінь) і $$t_2=8$$
Зворотна заміна $$2^x=8\Rightarrow 2^x=2^3\Rightarrow x=3.$$
Відповідь: 3.
Завдання 2.2
У скриньці лежить 12 білих і кілька чорних куль. Скільки чорних куль у скриньці, якщо ймовірність вийняти навмання чорну кулю дорівнює $$\frac{2}{5}$$?
Рішення
За визначенням імовірності $$P(A)=\frac{m}{n}$$, де $$m$$ – число сприятливих результатів (кількість чорних куль), $$n$$ – усіх результатів (кількість усіх куль). Тоді $$P(A)=\frac{m}{12+m}=\frac{2}{5}$$.
З пропорції отримаємо
$$5\cdot m=(12+m)\cdot2$$
$$5m-2m=24\Rightarrow 3m=24\Rightarrow m=8$$.
Відповідь: 8.
Завдання 2.3
Розв’язати рівняння $$\sqrt{x}+2\sqrt[4]{x}-8=0.$$
Рішення
ОДЗ: $$x\geqslant 0$$.
Заміна $$\sqrt[4]{x}=t\geqslant 0$$
$$t^2+2t-8=0$$
За теоремою Вієта:
$$t_1=-4$$ (сторонній корінь), $$t_2=2$$.
Зворотна заміна $$\sqrt[4]{x}=2\Rightarrow x=2^4\Rightarrow x=16$$.
Відповідь: 16.
Завдання 2.4
Вершини квадрата зі стороною 8 см належать сфері. Знайти площу сфери, якщо відстань від центру сфери до площини квадрата дорівнює 2 см.
Рішення
Виконаємо побудову. $$ABCD$$ – квадрат зі стороною 8 см, що знаходиться на відстані $$OO_1=2$$ см від центру сфери.
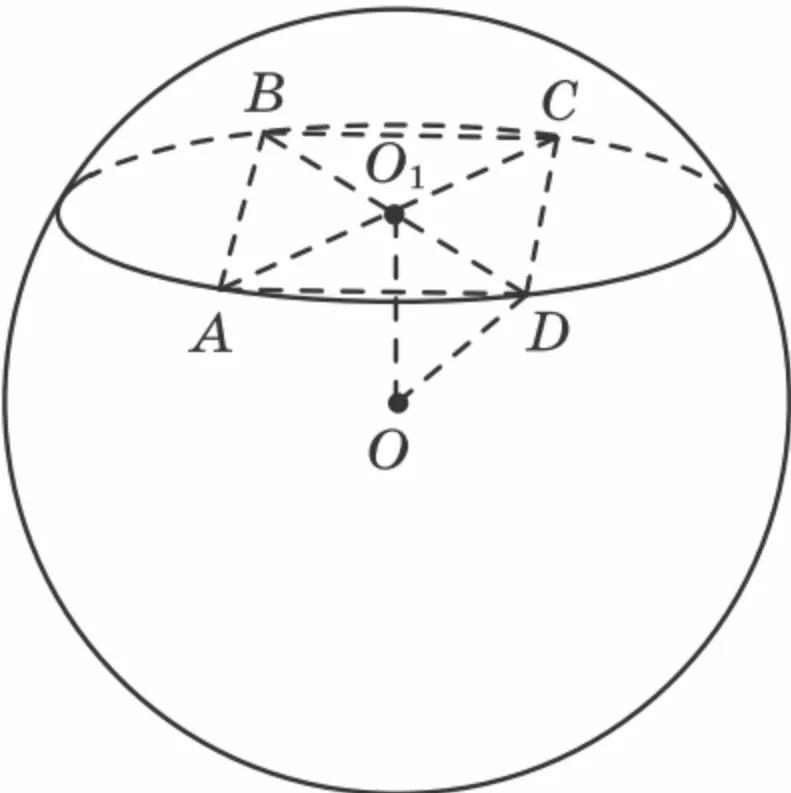
Діагональ квадрата за теоремою Піфагора дорівнює: $$BD=\sqrt{8^2+8^2}=8\sqrt{2}$$ см. Тоді $$O_1D=\frac{1}{2}BD=4\sqrt{2}$$ см.
З прямокутного трикутника $$OO_1D\;(\angle OO_1D=90^{\circ})$$ за теоремою Піфагора:
$$R=OD=\sqrt{OO_1^2+O_1D^2}=\sqrt{2^2+(4\sqrt{2})^2}=\sqrt{36}=6$$ см.
Знайдемо площу сфери:
$$S=4\pi R^2=4\pi\cdot6^2=144\pi$$ см2.
Відповідь: $$144\pi$$ см2.
Джерело: Збірник завдань для державної підсумкової атестації з математики: 11 кл. / О.С. Істер, О.І. Глобін, О.В. Комаренко. – К.: Центр навч.-метоод. л-ри, 2012.